The Fourier Transform and Derivatives

The Fourier Transform and Derivatives

함수 $f(x)$의 푸리에 변환과 푸리에 역변환 식은 다음과 같다.

 

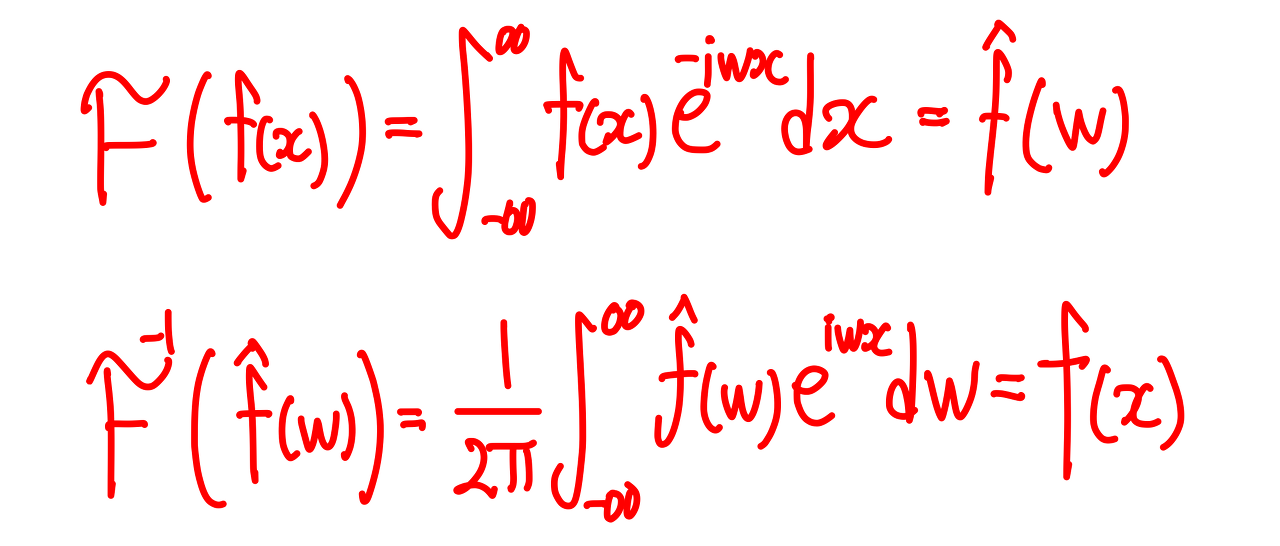
함수 $f(x)$ x에 대하여 미분한 것의 푸리에 변환을 구하는 과정은 다음과 같다.

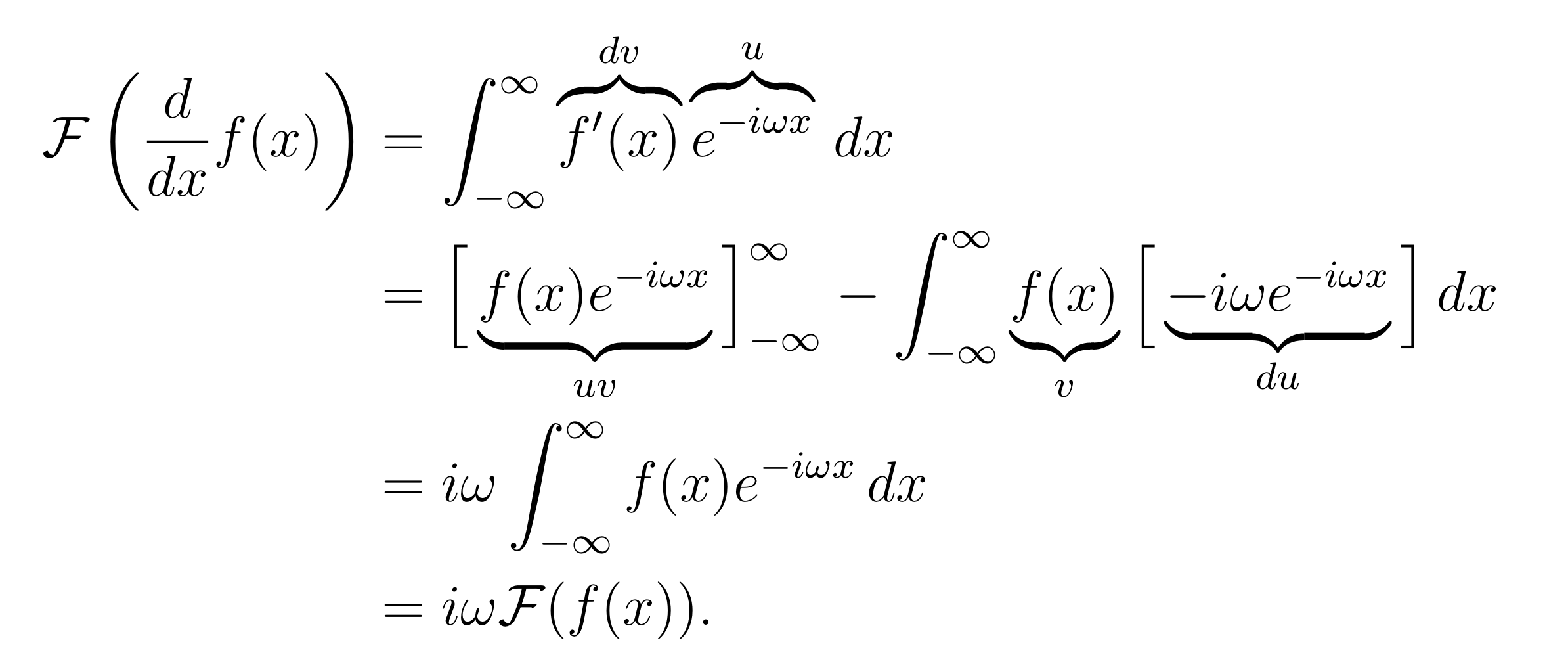
1. 푸리에 변환 식에 $f(x)$대신 $f'(x)$를 넣는다. 

2. $f'(x)$를 $dv$ $e^{-iwx}$를 $u$로 보고 부분적분을 한다.

 

함수 $f'(x)$의 푸리에 변환은 함수 $f(x)$를 먼저 푸리에 변환한 뒤 $iw$ 항을 곱해줌으로서 얻을 수 있다.

 

위와 같이 푸리에 변환시 미분항이 변환되는 성질을 이용하면 함수 $f(x)$가 미분 계산이 어려운 경우 푸리에 변환을 통해 함수 

$f'(x)$를 푸리에 변환한 것을 먼저 구한뒤 이를 푸리에 역변환 함으로서 함수 $f'(x)$의 미분을 얻을 수 있다.

 

 

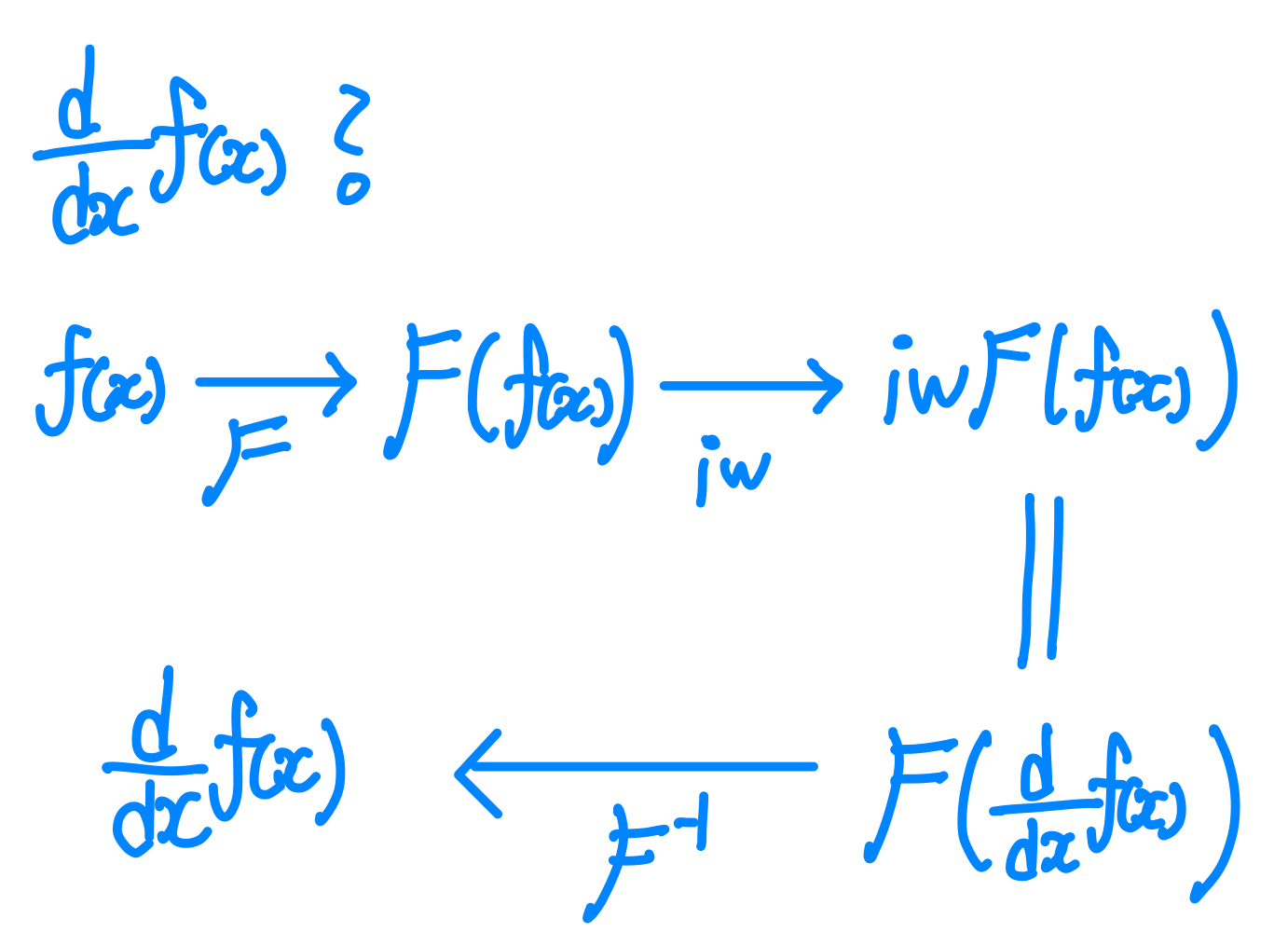
함수 $f(x)$가 domain $x$에서 $x$에 대한 변화를 측정하기 어려울 때 푸리에 변환을 통해 domain $w$에서 구한뒤 이를 역변환 하여 구하는 방법을 사용할 수 있다.

 

 

 

 

 

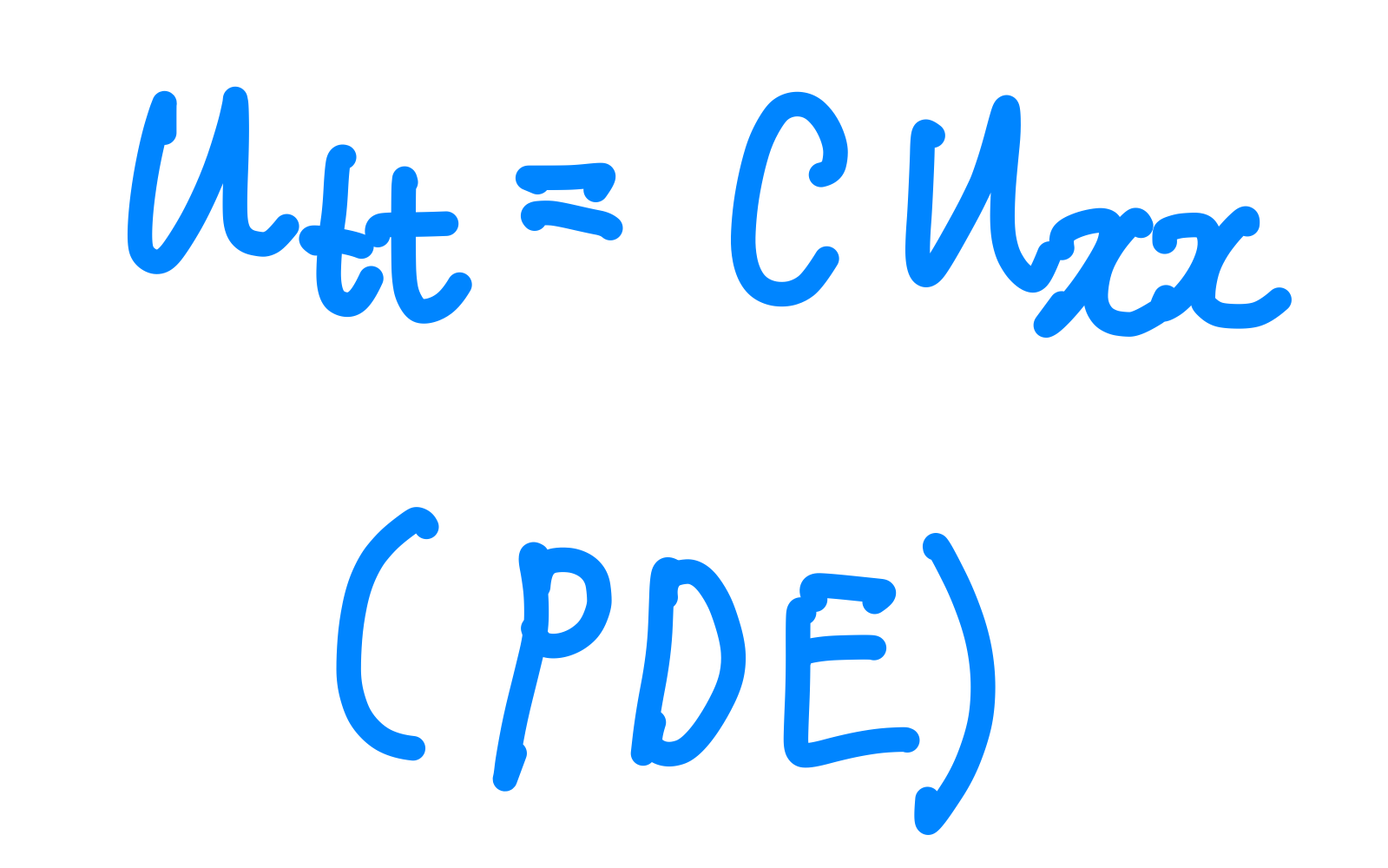
또한 위와 같은 파동 방정식이 편미분 방정식의 형태로 주어졌을 때 시간과 공간 변수 변화를 모두 고려해야 해서 다소 복잡하다.

이때 푸리에 변환에서의 미분의 특징을 이용하여 공간에 대하여 푸리에 변환을 하게 되면 시간에 대한 상미분 방정식으로 바뀌어 

고려해야할 변수가 시간만 존재하게 된다. 

 

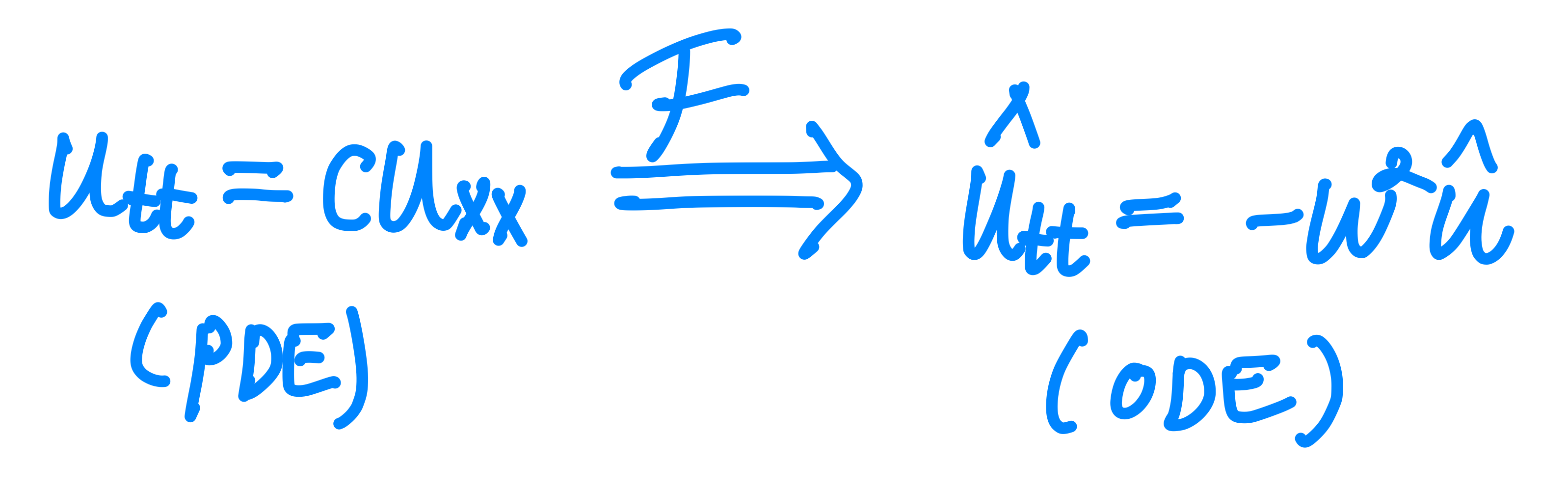
어떠한 미분방정식에서 여러 변수들에 대한 변화들을 고려해야 할 때

그 중 한 변수에 대해서 푸리에 변환하면 해당 변수에 대한 변화를 $iw$로 다룰 수 있게 되기 때문에 고려해야할 변수가 줄어든다. 

따라서 푸리에 변환한 공간에서 원하는 작업을 수행한 뒤 다시 역변환을 하는 방법을 이용하여 편미분 방정식을 풀 수도 있다.

 

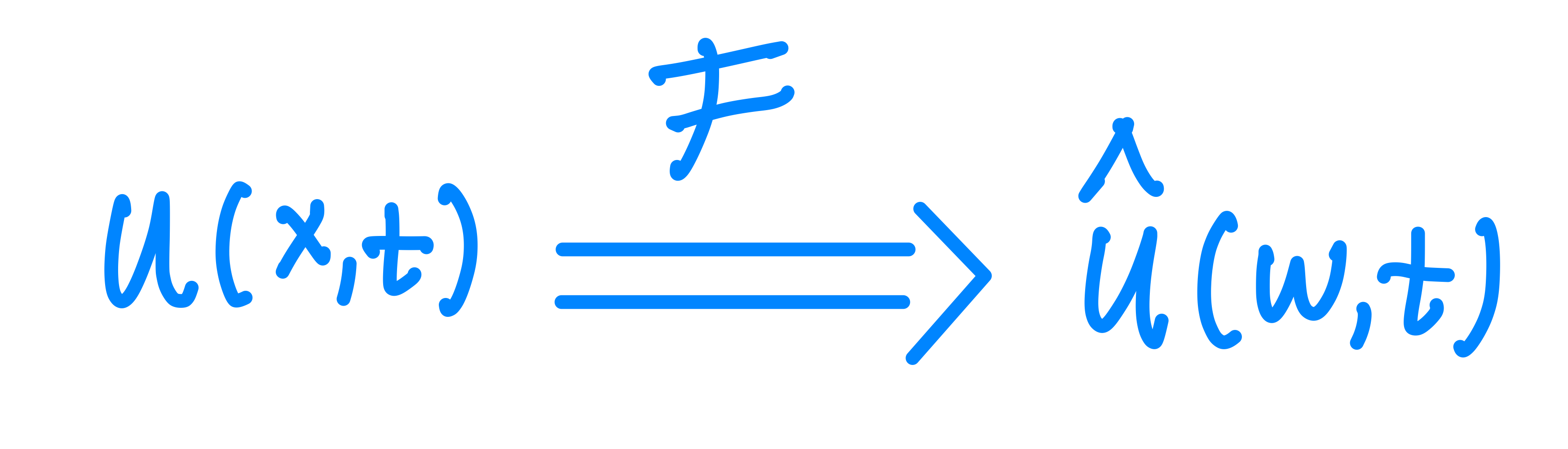
$x$ domain에서는 나타나는 $x$에 대한 변화는 $x$에 대해 푸리에 변환하면 $w$ domain에서 $iw$형태로 나타난다.

 

---