푸리에 급수/ 파이썬으로 확인하기

푸리에 급수 의미 생각 해보기 

푸리에 급수는 임의의 연속인 주기함수 $f(x)$ 를 여러 진동수 $k$로 분해하여 나타낸다.

이때 각 진동수는 실수범위 내에서 $coskx$ 와 $sinkx$ 를 직교 기저로 하여 표현된다. 

함수간의 내적은 두 함수가 얼마나 닮은가를 측정하므로 분해하려는 주기함수 $f(x)$를 $coskx$, $sinkx$ 와 내적하면 

진동수 $k$를 갖는 파장 중 어떠한 모양을 갖는 파장이 함수 $f(x)$에 들어있는지 알 수 있다. 

 

* 같은 진동수를 갖는 파장이더라도 파장의 구체적인 형태가 다를 수 있다.

   이러한 파장의 구체적인 형태는 $coskx$, $sinkx$의 크기 성분들을  조절하여 해당 모양을 나타낸다. 

 

즉 푸리에 급수를 통해 주기 함수를 나타내게 되면 해당 주기 함수가 어떠한 '진동수'들을 어떠한 '형태'로 가지고 있는지 알 수 있게 된다. 

 

아래와 같이 두가지의 함수가 주어졌을 때

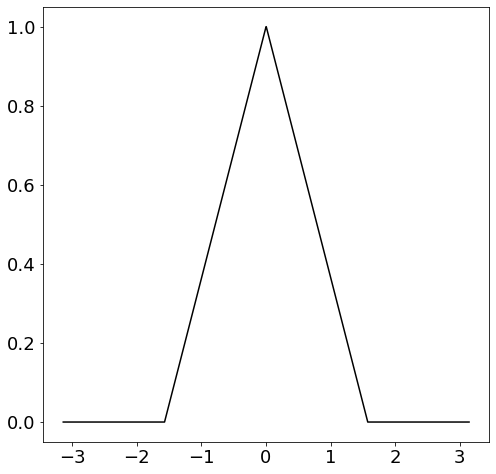
f1

f2

 

위의 두 함수를 푸리에 급수를 이용해 분해하여 진동수 k의 파형을 색을 구분하여 나타내면 아래와 같이 나타난다. 

 

f1

f2

 

색이 같은 파는 같은 진동수를 갖는다. 하지만 분해하는 함수에 따라 파형이 확연히 다른 모습을 볼 수 있다. 

이는 분해하려는 함수와 기저 $sin(kx), cos(kx)$ 간의 내적을 통해 해당 함수들이 갖는 각 진동수 k에 대한 파형을 구하였기 때문이다.

 

 

위의 식들은 함수 $f(x)$를 푸리에 급수로 분해할 때의 식을 나타낸다. 

진동수 k는 $coskx$ 와 $sinkx$ 기저의 결합으로 나타나며

각 기저의 성분 $A_k, B_k$은 함수 $f(x)$와 기저간의 내적을 통해 나타나는 것을 알 수 있다.

 

 

위와 같이 진동수 k를 증가시키며 함수 $f(x)$를 각 진동수들로 분해한다. 

또한 분해된 진동수들은 각각 $coskx$ 와 $sinkx$ 결합으로 나타나는 것이다. 

 

 

 위의 식들은 주기 $2\pi$에 대해서 나타낸 것이다. 주기 $L$에 대해서 일반화하면 다음과 같이 나타난다. 

 

---

 

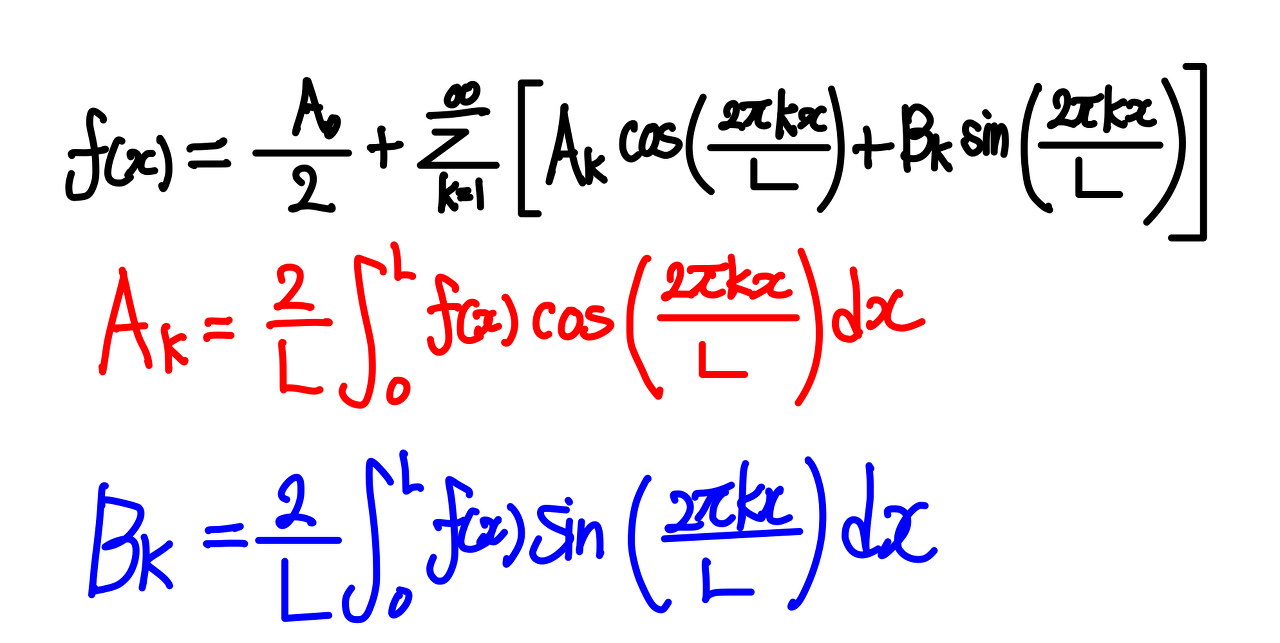
Python을 활용한 계산

위의 식을 활용하면 실제로 주기 함수를 여러 진동수로 분해할 수 있을까?

이를 확인하기 위해서는 여러 진동수로 분해되어 나타나는 값들을 다시 더해서 원래의 함수 $f(x)$가 나오는지를 보면 된다.

 

분해할 함수 f(x)

# 값 계산 및 결과를 graph로 나타낼 libaray import
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.cm import get_cmap

# graph가 나타날 Board 조정
plt.rcParams['figure.figsize'] = [8, 8]
plt.rcParams.update({'font.size': 18})

# 함수 f(x)가 input으로 받을 값인 정의역을 정의 
dx = 0.001
L = np.pi
x = L * np.arange(-1+dx, 1+dx, dx)
n = len(x)
n_quart = int(np.floor(n/4))

# 분해할 함수 f(x)
f = np.zeros_like(x)
f[n_quart:2*n_quart] = (4/n)*np.arange(1, n_quart+1)
f[2*n_quart:3*n_quart] = np.ones(n_quart) - (4/n)*np.arange(0, n_quart)

# f(x) graph로 띄우기
fig, ax = plt.subplots()
ax.plot(x, f, '-', color='k')

 

분해할 함수 f(x)

각 진동수로 분해하기

# 나타날 graph의 색 조정
name = "Accent"
cmap = get_cmap('tab10')
colors = cmap.colors
ax.set_prop_cycle(color=colors)

# k=20 까지만 f(x)를 각 진동수로 분해  
A0 = np.sum(f * np.ones_like(x))*dx
fFS = A0/2
A = np.zeros(20)
B = np.zeros(20)
for k in range(20):

    A[k] = np.sum(f * np.cos(np.pi * (k + 1) * x / L)) * dx
    B[k] = np.sum(f * np.sin(np.pi * (k + 1) * x / L)) * dx
    fFS = fFS + A[k]*np.cos((k+1)*np.pi*x/L) + B[k]*np.sin((k+1)*np.pi*x/L)
    ax.plot(x, fFS, '-')

 

for 문을 보면 각 루프마다 푸리에 급수로 나타낸 fFS가 새로운 진동수가 더해지면 갱신되고 있음을 알 수 있다. 

식에서는 진동수를 무한히 늘려가면서 급수를 실제 함수 $f(x)$에 수렴시키지만 현실적으로는 계산 횟수에 한계가 있으므로 20회만 진행하였더니 위와 같은 그래프를 얻을 수 있었다. 처음 파란색 그래프에서 시작해서 초록색 그래프에 이르기까지 새로운 진동수들이 더해질 때마다 우리가 분해하였던 함수 $f(x)$에 가까워짐을 알 수 있다. 

 

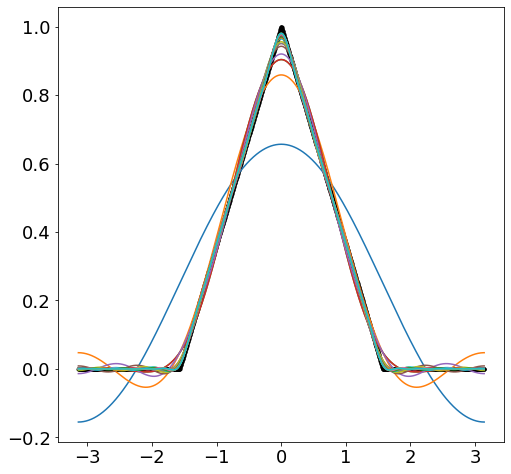
검은색이 함수 f(x)

 

분해할 진동수 k의 개수에 따른 오차 분석

위의 그림과 같이 진동수를 늘려 갈수록 분해한 함수 $f(x)$에 푸리에 급수가 근사하는 확인하기 위해서

이 둘의 차이를 norm을 이용해 계산하고 차이가 감소하는지를 확인해 보았다. 

# 들어갈 값의 갯수만큼 자리 마련해 놓기
fFS = (A0/2) * np.ones_like(f)
kmax = 100
A = np.zeros(kmax)
B = np.zeros(kmax)
ERR = np.zeros(kmax)

# 함수 및 오차 값 계산
A[0] = A0/2
ERR[0] = np.linalg.norm(f-fFS)/np.linalg.norm(f)

for k in range(1, kmax):

    A[k] = np.sum(f * np.cos(np.pi * k * x / L)) * dx
    B[k] = np.sum(f * np.sin(np.pi * k * x / L)) * dx
    fFS = fFS + A[k]*np.cos(k*np.pi*x/L) + B[k]*np.sin(k*np.pi*x/L)
    ERR[k] = np.linalg.norm(f-fFS)/np.linalg.norm(f)


thresh = np.median(ERR)*np.sqrt(kmax)*(4/np.sqrt(3))
r = np.max(np.where(ERR > thresh))


# 계산 값 graph로 나타내기
fig, axs = plt.subplots(3,1)
axs[0].semilogy(np.arange(kmax), A, color='b')
axs[0].semilogy(r, A[r],'o', color='k')
plt.sca(axs[0])
plt.title('Fourier cosine Coefficients')

axs[1].semilogy(np.arange(kmax), B, color='r')
axs[1].semilogy(r, B[r],'o', color='k')
plt.sca(axs[1])
plt.title('Fourier sine Coefficients')


axs[2].semilogy(np.arange(kmax), ERR, color='g')
axs[2].semilogy(r, ERR[r],'o', color='k')
plt.sca(axs[2])
plt.title('Error')

plt.subplots_adjust(left=0.125, bottom=0.1,  right=0.9, top=0.9, wspace=0.2, hspace=0.9)


plt.show

 

 

첫번째와 두번째 그래프는 각 진동수 k를 구성하는 기저 $cos$와 $sin$의 성분을 나타낸다.

그래프를 분석하여 보면 특정 진동수 k들에서는 기저들의 성분이 0인것으로 보아 해당 주파수들은 가지고 있지 않음을 알 수 있다. 

분해한 함수 $f(x)$가 각 주기의 앞부분과 뒷부분에서 0의 함수 값을 가지기 때문에 여러 주파수 성분을 함수 $f(x)$가 가지지 않는 것을 역으로도 확인할 수 있다. 

 

세번째 그래프는 주파수를 분해하는 진동수의 종류 수를 늘려 나갈 때 실제 함수 $f(x)$와 푸리에 급수간의 차이가 어떻게 되는지를 나타낸다. 푸리에 급수에 더해지는 주파수 k를 늘려 나갈수록 Error가 감소하는 것을 볼 수 있다.

이를 통해 분해하는 진동수의 종류 수를 늘려나감에 따라 실제 함수 $f(x)$에 수렴하는 것을 확인할 수 있다.

 

 

푸리에 급수를 이용하면 임의의 주기함수 $f(x)$를 여러 진동수 k로 분해하여 나타낼 수 있음을 확인하였다.

각 진동수 k는 $cos(kx)$ 와 $sin(kx)$를 기저로 하여 이들의 결합으로 나타났다.

이때 각 진동수의 기저와 분해할 함수 $f(x)$를 함수간의 내적을 통하여

해당 진동수를 갖는 파장 중 함수 $f(x)$에 들어있는 파장의 형태가 어떻게 구성되어 있는지 알 수 있다. 

 

---