푸리에 변환에 대하여

푸리에 급수 

푸리에 급수란 임의의 주기 함수 $f(x)$를 각 진동수 $k$로 분해하는 과정이다.

 

분해된  각 진동수 $k$는 실수 영역에서는 sin 과 cos를 기저로 하여 함수  $f(x)$와 내적을 통해서 해당 진동수를 갖는 파 중 함수 $f(x)$를 구성하는 특정 $k$ 진동수의 파형을 나타내었다.

 

복소수 영역에서는 각 진동수 $k$를  $\psi_k$($k$는 서로 다른 정수)를 직교 기저로 하여 함수 $f(x)$와의 내적을 통하여 파형을 나타 내었다.

---

- 주기가 $2\pi$인 경우 푸리에 급수의 형태

 

 

- 일반화한 주기가 $L$일때 푸리에 급수의 형태

 

- 복소수 공간에서 서로 직교하는 $\psi_k$를 직교 기저로 하여 각 진동수 $k$를 분해하였을 때 푸리에 급수의 형태

( * 주기를 $2L$로 하여 푸리에 급수의 형태를 약간 변화 )

---

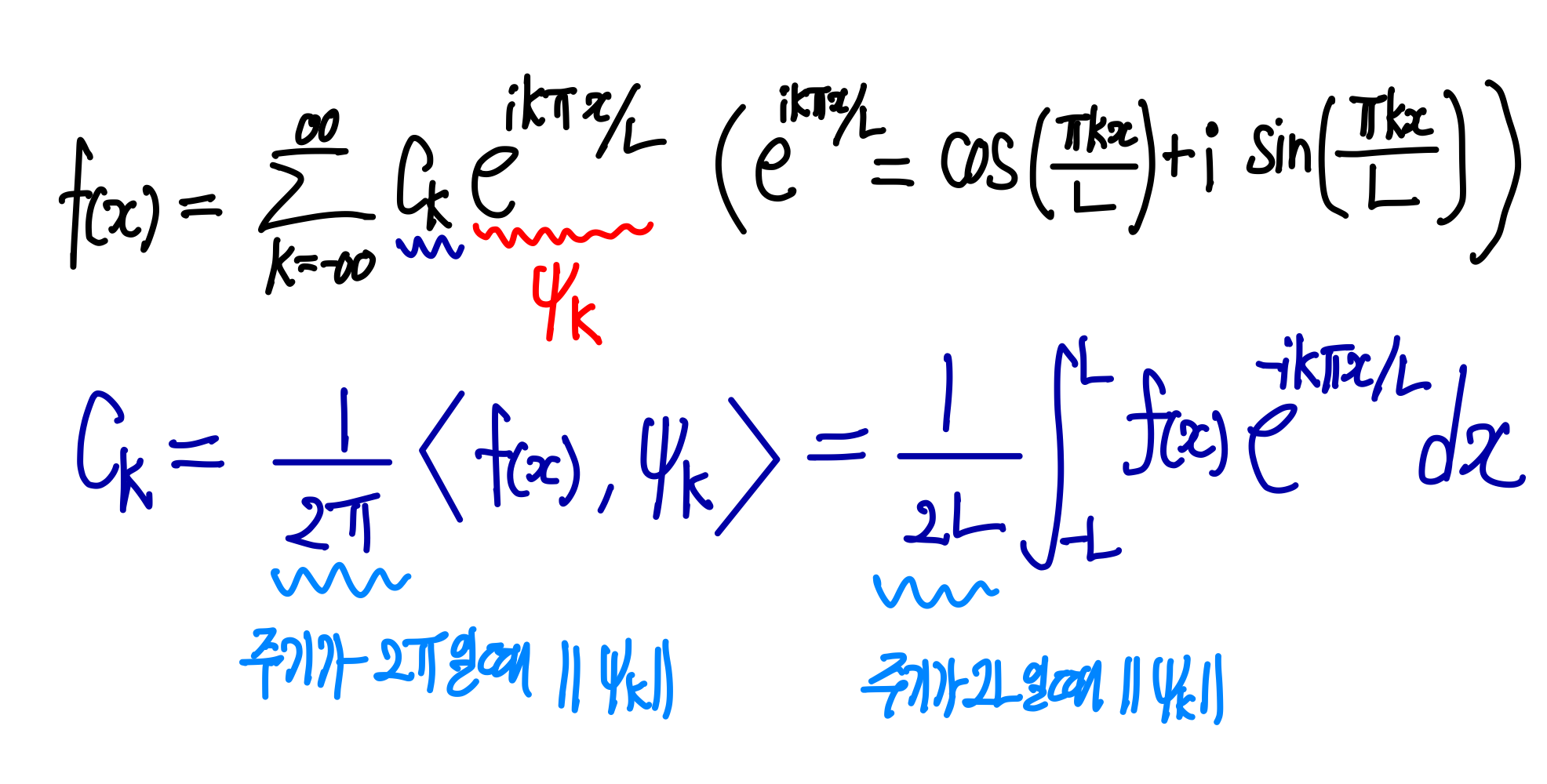
푸리에 변환

복소수 영역에서 푸리에 급수를 전개하면 위에서 나타냈듯이 주기가 $2L$인 주기 함수를 각 진동수 별로 분해하여 나타낼 수 있었다.

 

만약 주기를 무한대로 늘린다면 어떻게 될까?

 

주기란 어떠한 현상이 일어난 뒤 해당 현상이 되풀이 될때까지의 기간을 의미한다. 

 

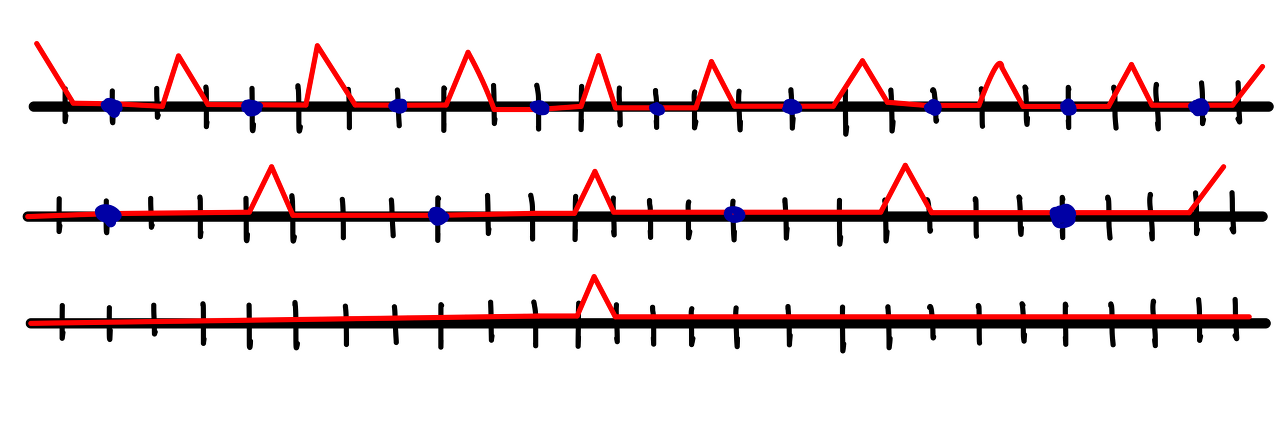
위의 그림에서 나타냈듯이 주기적인 현상이 주어졌을 때 

주기를 늘리다보면 현상이 반복되기 까지 걸리는 시간이 길어지다가 주기가 무한해지면 해당현상 자체만 남게된다.

이것을 point로 하여 푸리에 급수에서의 주기함수의 주기를 무한히 보내보자

 

복소수 영역에서의 푸리에 급수는 아래와 같이 나타난다. 

위의 푸리에 급수 식에서 각 기저함수 $\psi_k=e^{ik\pi/L}$에서 진동수를 나타내는 부분인 $k\pi/L$를 $w_k$라 하자.

 

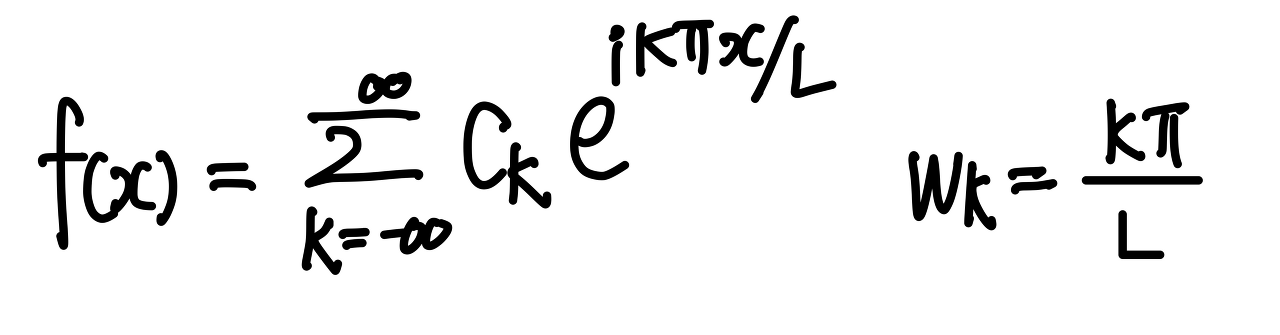
진동수는 주기적인 현상이 단위 시간 동안 몇번 일어났는가를 의미한다.

주기는 해당 현상이 반복되기 까지의 시간을 의미하므로 주기와 진동수는 반비례 관계임을 알 수 있다.

 

예를 들어 진동수가 10HZ 일때 1초에 주기적 현상이 10번 일어나며 이때 주기는 0.1초로 주기적 현상이 0.1초마다 한번씩 일어난다. 

이때 주기가 2배가 되어 0.2초마다 주기적 현상이 일어난다면 1초동안 발생하는 주기적 현상은 5번이다. 

즉 주기가 길어질수록 진동수가 작아지다가 주기가 무한해지면 반복적인 현상이 일어나지 않고 현상 자체만 남게 된다. 

이는 진동수가 주기적 현상이 일어난 횟수를 의미하므로  '주기성'을 상실하여 진동수는 0으로 가는 것을 의미하게 된다. 

 

진동수 $w_k$에서 다음 진동수 $w_{k+1}$까지의 차이를 $\Delta w$라 했을 때 $\Delta w$는 $\frac{\pi}{L}$이다.

 

주기가 무한해짐에 따라서 $\Delta w$는 0으로 수렴한다. 이는 각 진동수간의 차이가 사라지는 것을 의미한다.

  

* 푸리에 급수에서 각 진동수 $k$로 분해된 파들은 진동수에 따라 구분되는데

  주기가 무한해지면서 각 파들 사이에 진동수로 인한 구분이 사라지고 분해된 파들은 파형 자체만 남게 된다. 

(주기적인 현상은 하나의 현상이 반복되는 것임을 알고 있기 때문에 반복되는 요소를 제하면 분해된 현상 자체에 대해서 다룰 수 있게 된다.)

 

 

함수 $f(x)$를 푸리에 급수를 이용해 나타내면 아래와 같이 나타난다. 

(푸리에 급수로 표현된 상태는 함수 $f(x)$을 구성하는 각 진동수 $k$ 파들로 분해하여 나타낸 상태이다.)

 

 

여기서 $L$을 $\Delta w$로 바꾸면 위의 식은 아래와 같이 바뀐다.

 

 

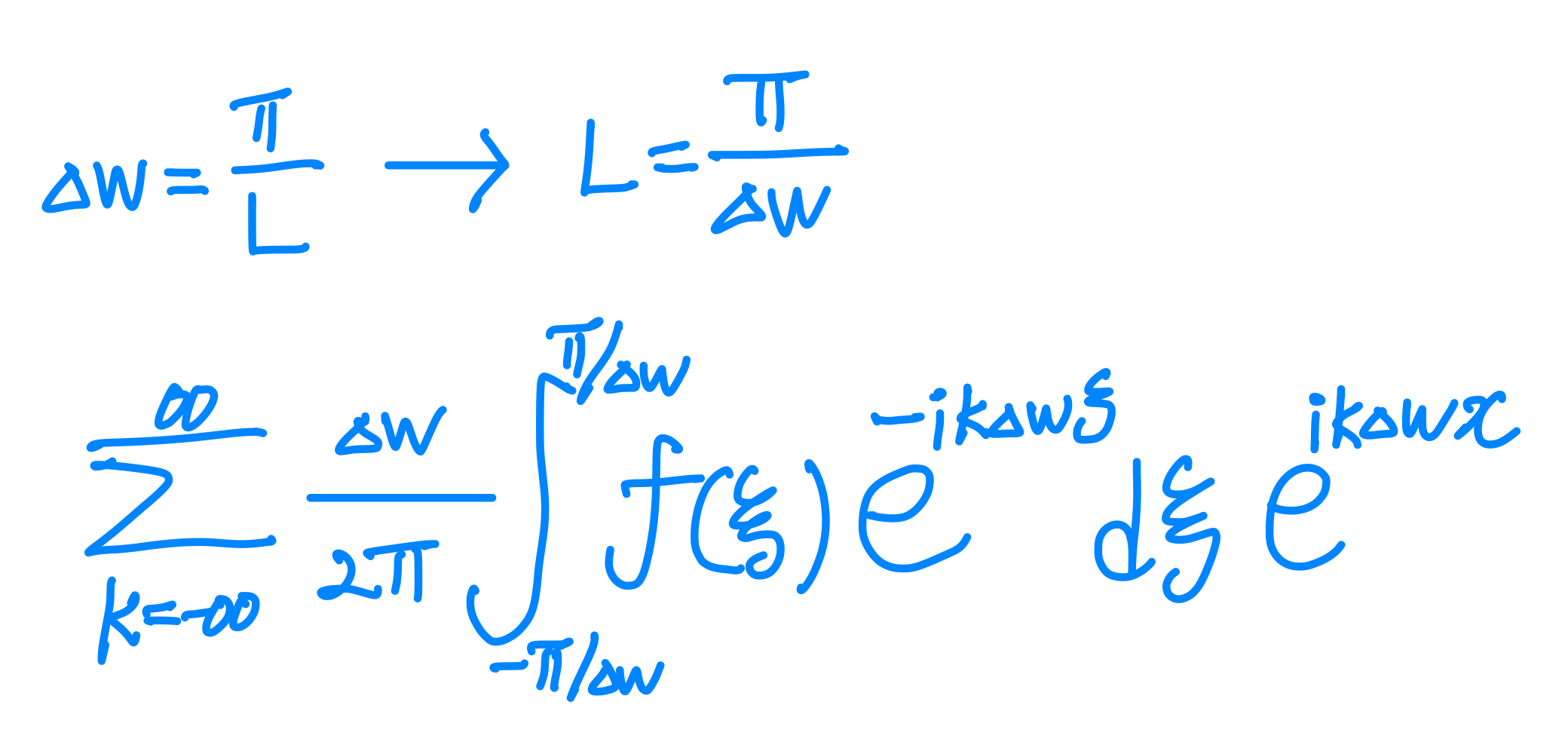
아직은 위의 식을 $\Delta w$에 대해  표현한 것이지 아무것도 한 것이 없다. 

이제 위의 식에서 주기를 무한대로 보내면 위에서 언급한 것과 같이 $\Delta w$가 0으로 가게 된다.

 

그러면 아래와 같이 식을 나타낼 수 있다. 

 

 

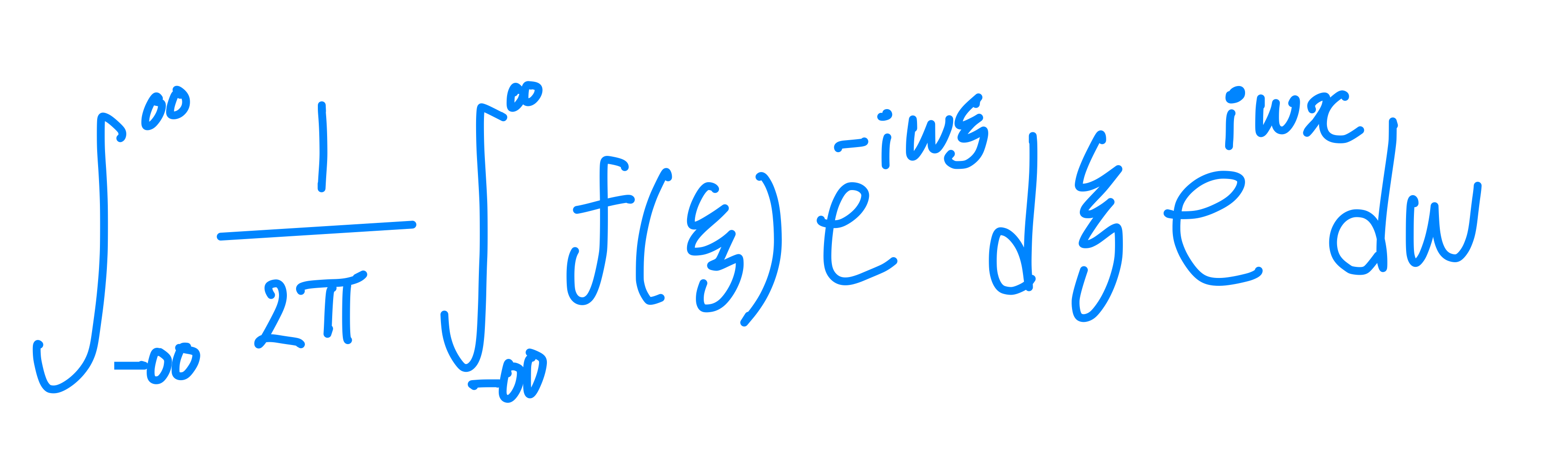
순서를 다시 정리하여 나타내면 안쪽 적분 부가 함수 $f(x)$를 푸리에 변환한 상태가 된다. 

만약 단위 시간에 대해서 공간상에서 주기적인 현상이 일어나는 경우

주기가 무한해짐에 따라 무한한 시간 동안 현상은 단 한번 나타나게 된다.

따라서 시간 축은 무의미해져 시간축이 사라지고 공간상의 움직임만 공간축상에 남게 된다.

 

 

- 푸리에 변환과 푸리에 역변환 식

---

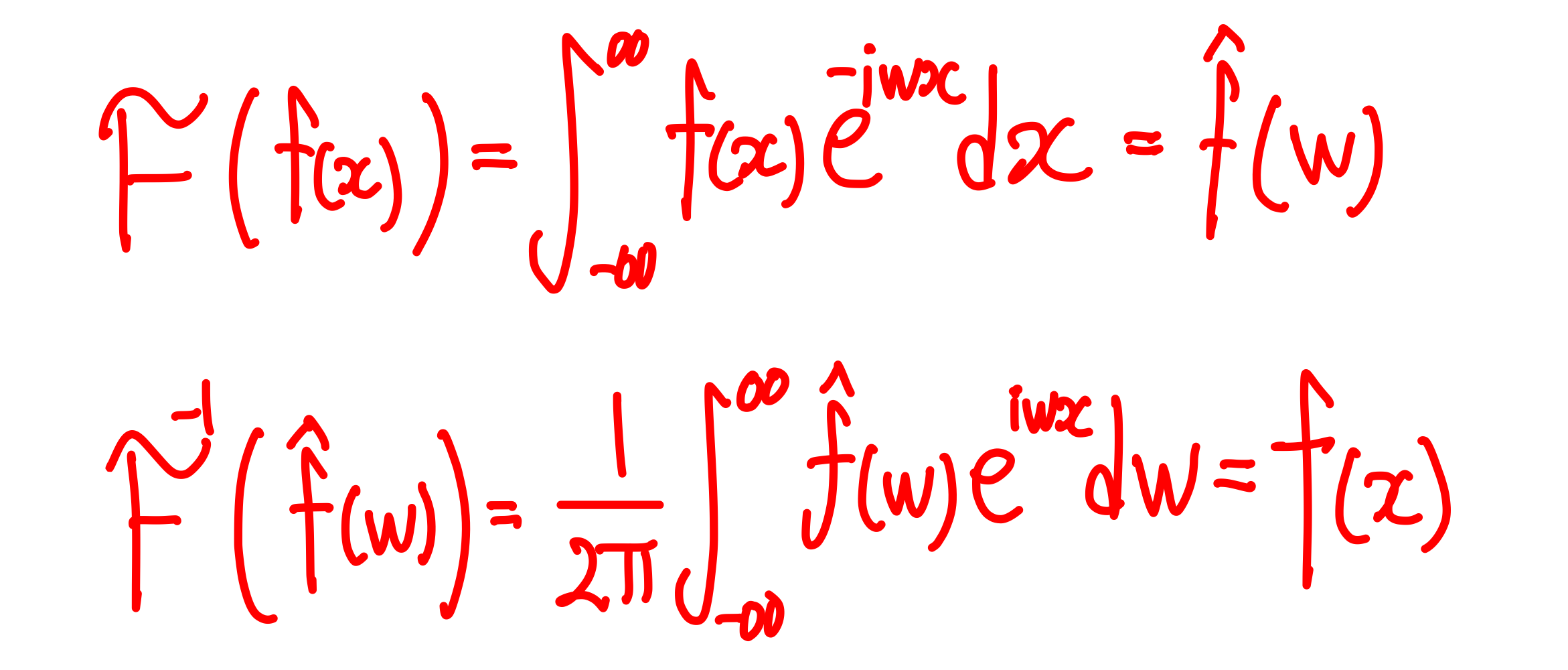
푸리에 변환에 대한 감상

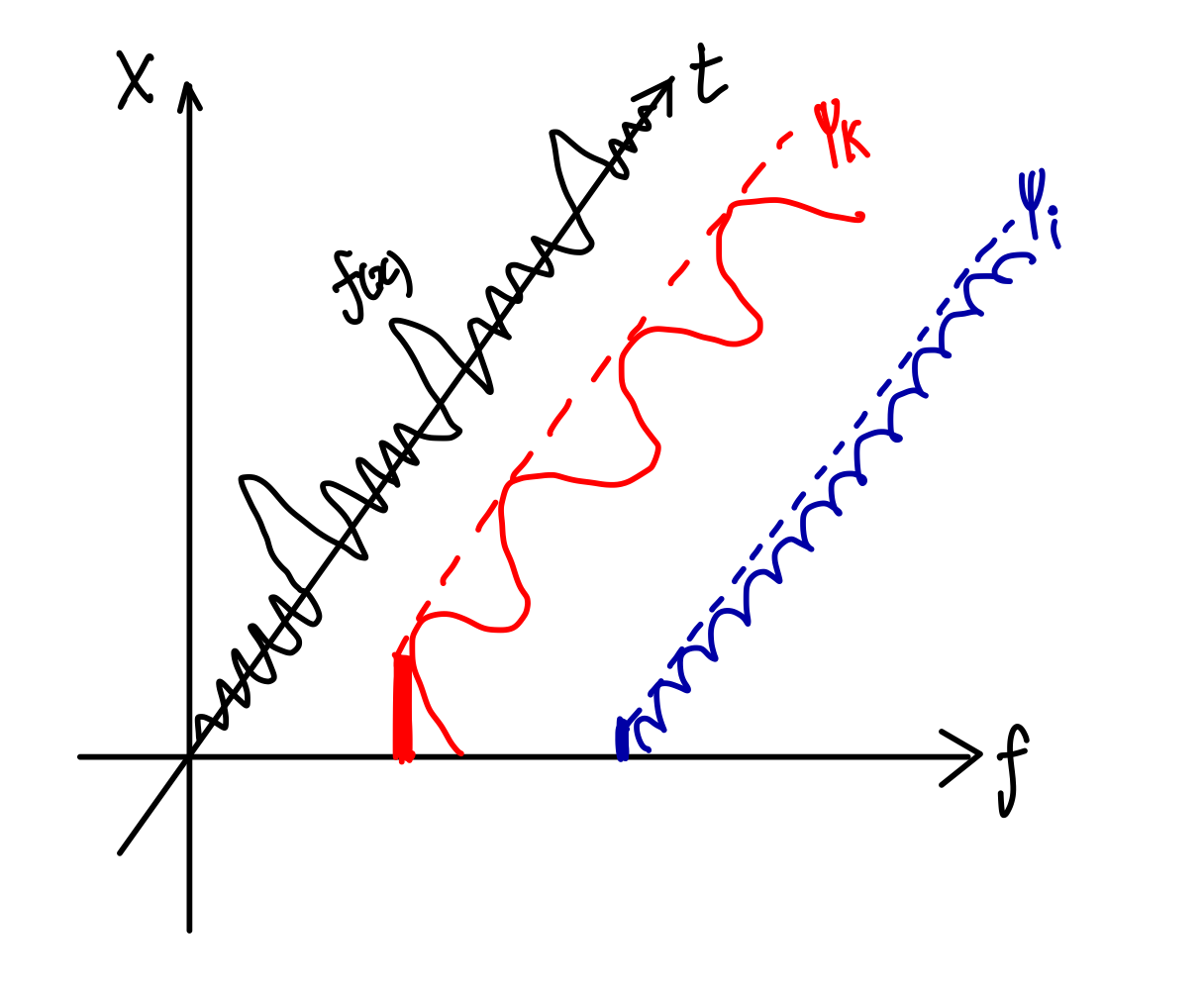
푸리에 급수를 통해서 함수$f(x)$를 각 진동수별로 분해하였다.
'진동수는 주기적인 현상이 단위시간동안 몇번 반복되었는가?'
주기를 무한대로 함에 따라 해당 현상의 주기성이 사라지고 현상 자체만 남게 된다.
위에서 분해된 파장의 시간에 따라 공간상(x축)에서 움직임이 나타났는데 주기를 다음 움직임이 나타날 때까지의 기간으로 포괄적으로 해석하면 해당 파장들은 공간상에서 정지한 것과 같게 된다. 따라서 시간이 흐르지 않은 것과 같게 되고 시간축이 의미를 상실한다.
따라서 공간축에 파장을 사영하여 분해된 파장들은 공간상에서의 흔적으로서만 의미를 갖게된다.
즉 푸리에 변환을 통해 분해된 진동수는 공간상에서의 주파수 성분들로 나타난다.

주기성을 갖는 함수 f(x)를

푸리에 급수를 이용해 각 진동수별로 분해한뒤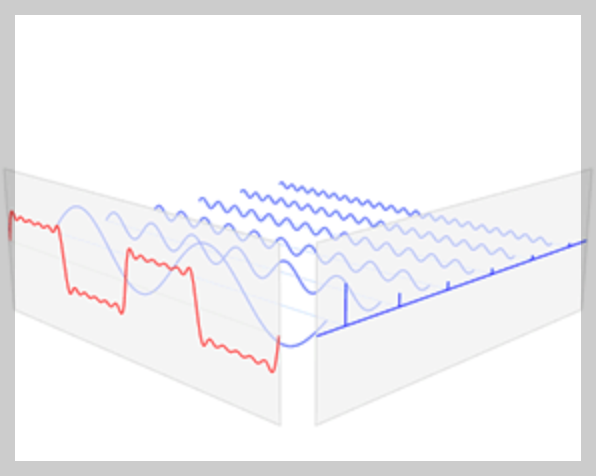

주기를 무한대로 하여 각 진동수를 공간축상에 사영시키면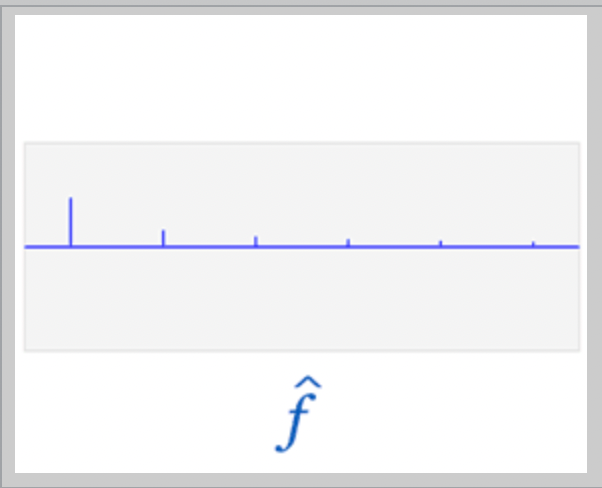

 

각 진동수가 공간성분만 나타난다.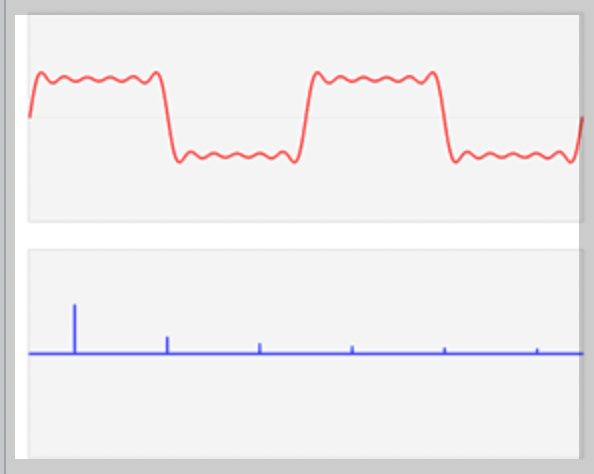

함수 f(x)를 푸리에 변환하면 분해된 각 진동수가 주기성을 잃고 해당 진동수를 가졌던 파의 형태만 남게 된다.

 

시공간상에서의 현상은 시간에 따라 서술되는데 시간이 무한해지면 현상은 공간 자체로 편입된다?

---