합성 곱과 푸리에 변환

Convolution

합성곱 (convolution)은 하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음

구간에 대해 적분하여 새로운 함수를 구하는 연산자이다.

 

두개의 함수 $f$와 $g$가 있을 때 두 함수의 합성곱은 다음과 같이 나타난다.

합성곱 연산은 두 함수 f, g 가운데 하나의 함수를 반전(reverse), 전이(shift)시킨 다음, 다른 하나의 함수와 곱한 결과를 적분하는 것을 의미한다. 위의 경우에는 함수 $g$를 반전후 전이시킨 경우이다.

위와 같이 나타내면 함수 $f$를 반전후 전이시킨 경우이다.

 어떠한 함수를 반전후 전이시켰는지와 상관없이 두 식은 형태는 다르지만 항상 같은 값을 갖는다.

 

 

함수 $f(t)$와 $g(t)$가 위와 같이 주어졌다.

이 함수들을 시간에 대한 입력이라고 생각하면 $f(t)$의 경우에는 0초부터 입력이 시작되며 $g(t)$는 그로부터 1초 뒤 부터 입력이 시작된다.

위의 입력들을 합치기 위해서 둘중 하나를 반전 후 전이시킨다.  

 

0초일때 $f$에 의해서 주어진 입력은 1초뒤 입력된 $g$에 영향을 받는다. 

 

$g$가 $f$를 가로지르면서 $f$와 $g$가 합성되어 새로운 형태의 입력을 갖는다.

 

합성곱을 활용하면 위와 같이 입력 시스템 상에서 간격을 두고 발생하는 입력들이 서로에게 영향을 주어 새로운 형태의 입력이 출력된다.

 

또한 함수 $f$와 $g$를 무엇으로 보냐에 따라 시스템의 형태가 달라진다.

함수 $g$를 $f$를 필터링하는 경우 필터 시스템이 될 수도 있고

함수 $g$가 $f$를 입력으로 받아 출력하는 경우 입출력 시스템이 되는 것 같이 다양하게 활용 될 수 있다.

---

푸리에 변환을 이용하여 합성곱 구하기

함수 $f$와 $g$의 합성곱을 구하기 어려운 경우 푸리에 변환을 이용하여 구하는 방법을 이용해 볼 수 있다.

 

$f$ 와 $g$ 합성곱의 푸리에 변환은 $f$ 와 $g$를 각각 푸리에 변환한 뒤에 둘을 곱한 것과 같다.

따라서 각각의 함수를 푸리에 변환한 뒤 곱한 것을 푸리에 역변환하게 되면 원하는 함수들의 합성곱을 얻을 수 있다.

 

위의 식이 성립하는지 확인하기 위해서 각각 푸리에 변환된 것들에 곱의 푸리에 역변환이 합성곱이 나오는지를 보면 된다.

 

 

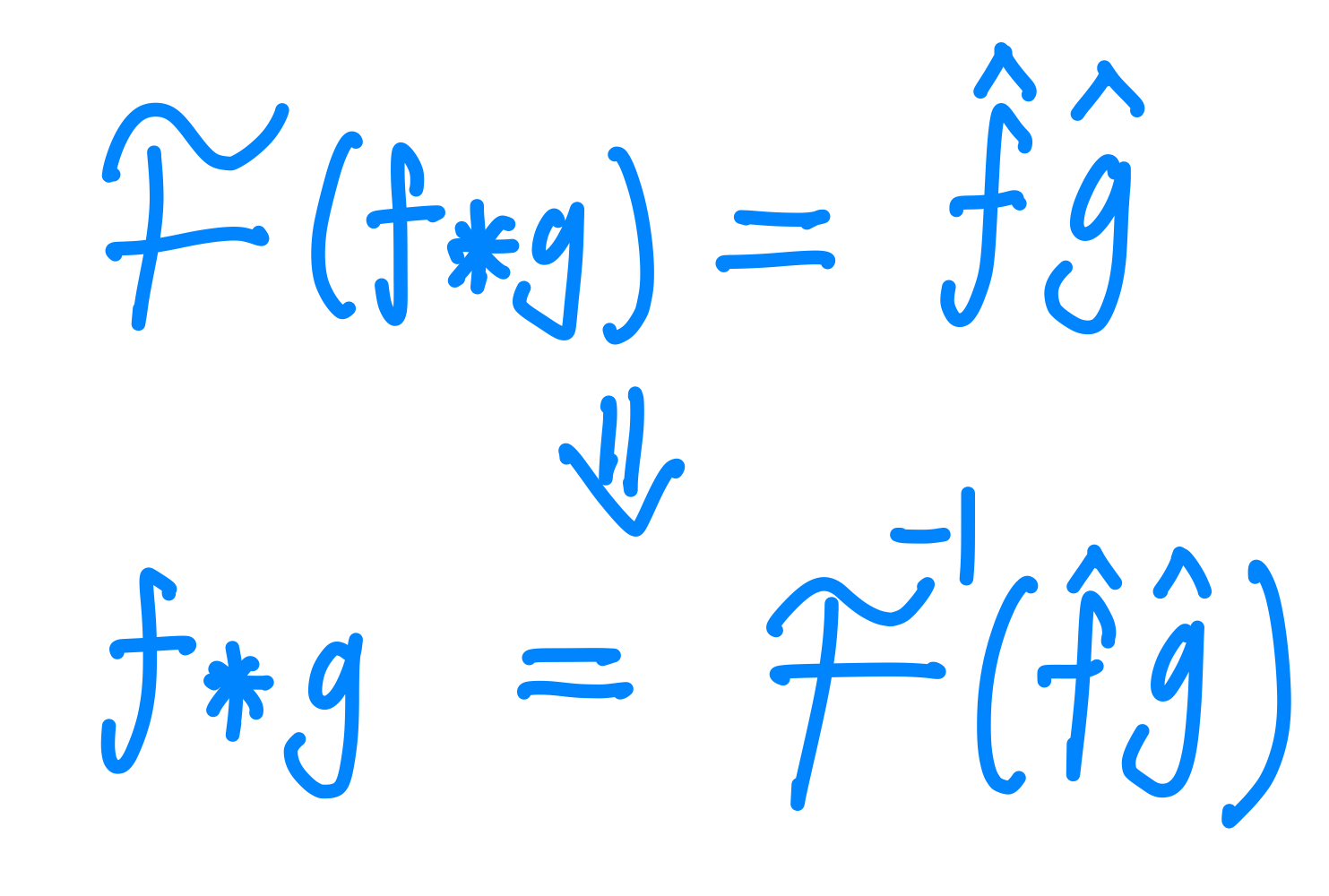
푸리에 변환과 역변환 식이 주어졌을 때 

이를 이용해서 각각 푸리에 변환된 $f$와 $g$의 곱을 푸리에 역변환하면 다음과 같다.

위에서 나타난 푸리에 역변환 과정을 거치고 나면 푸리에 변환된 각 함수의 곱이 푸리에 역변환을 통해서 합성곱이 되는 것을 알 수 있다.

---