-
Discrete Fourier Transform (DFT)Math♾️/Fourier Analysis 2022. 9. 15. 22:11
DFT
해석 함수가 존재할 때에는 푸리에 변환식에 이를 넣어 계산하면 되지만 현실에서는 많은 경우 실험과 측정을 통해서 데이터를 얻게 된다.
따라서 해석 함수의 형태가 아닌 이산적인 데이터의 나열을 푸리에 변환하기 위한 방법이 필요하게 된다.

위와 같이 함수 $f(x)$가 연속인 해석함수로 주어졌을 때 이를 푸리에 변환 식에 대입하면 푸리에 변환을 할 수 있었다.


하지만 위의 빨간색 점과 같이 데이터가 이산적으로 존재하게 되면 이를 푸리에 변환식을 이용하기 어렵다.
따라서 이산적 데이터를 푸리에변환하는 방법이 필요하게 된다.
해석적 함수의 경우 전체함수에 대하여 한번에 각 진동수를 갖는 파형으로 분해하였다면
이산적 데이터의 경우에는 각 데이터점이 어떠한 진동수를 가지고 있는지 분해하여 동일한 진동수끼리 더해주어야
전체 데이터들이 어떠한 진동수를 얼마나 가지고 있는지 알 수 있다.
각 데이터점이 가지고 있는 진동수 성분을 분해하는 식은 아래와 같다.
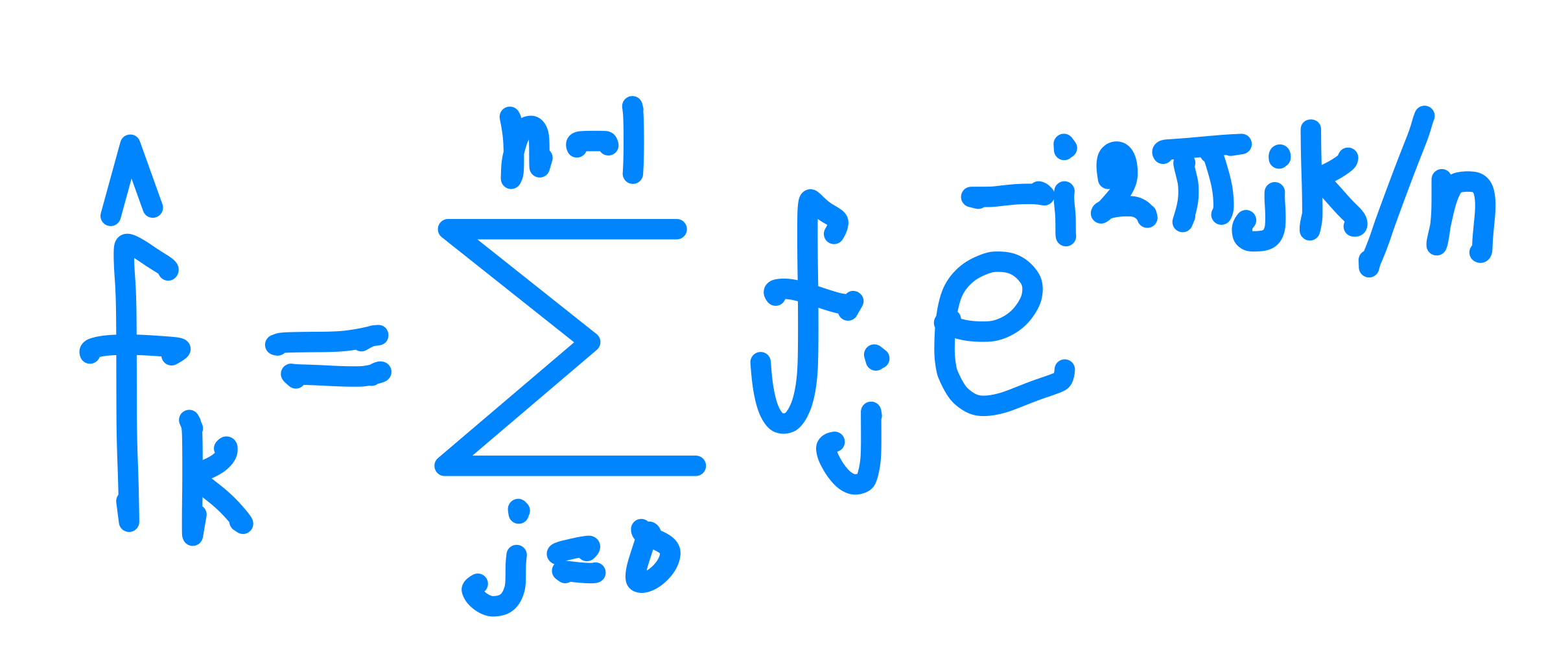
$j$는 데이터점의 순서를 의미하며 $k$는 진동수가 $k$인 경우를 의미한다.
푸리에 변환된 $k$ 진동수 성분은 첫번째 부터 마지막까지의 데이터점들을 구성하는 진동수들 중에 진동수 $k$성분을 추출하여 모두 더한것이다.
위의 식을 좀더 간단히 표현하면 아래와 같이 나타낼 수 있다.

각 데이터 점들과 이를 푸리에 변환한것을 하나의 열벡터로 나타내면 아래와 같이 나타난다.
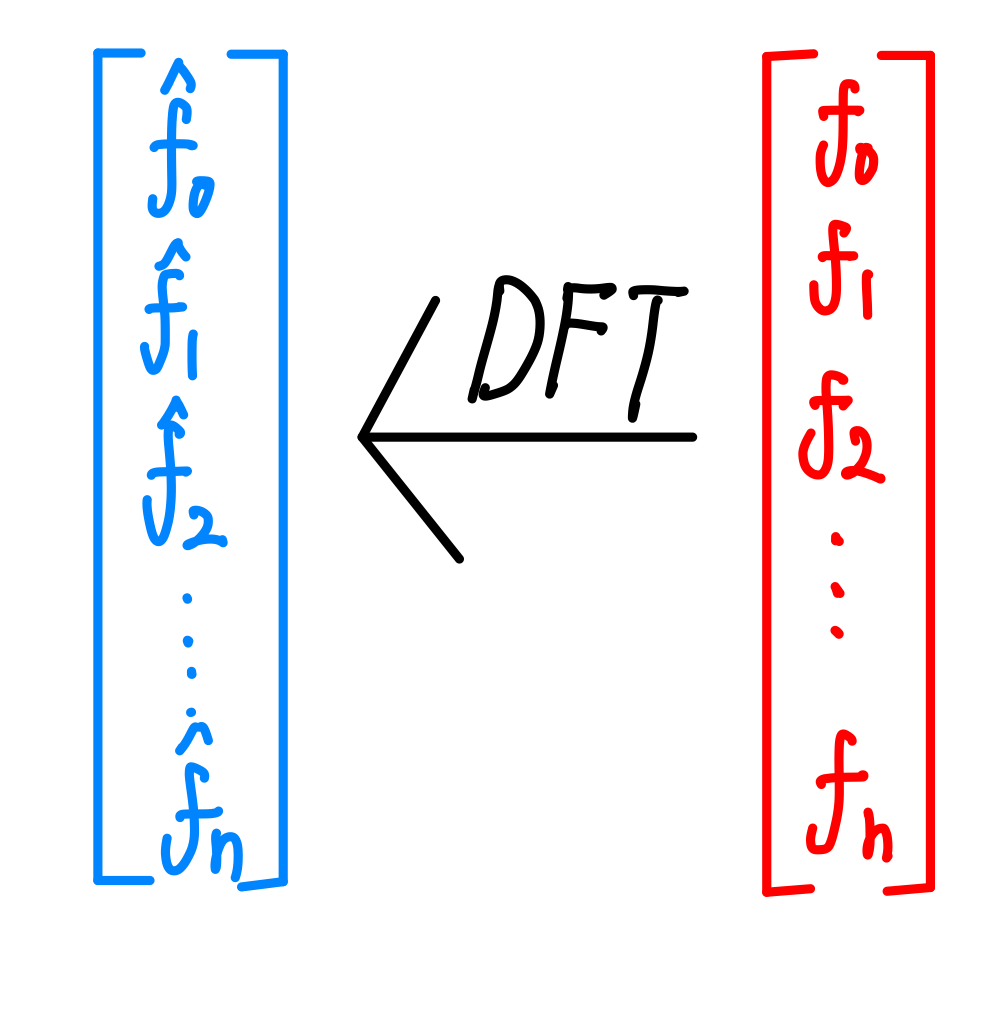
위와 같이 열벡터로 나타나게 되면 이 둘사이의 관계를 행렬로 나타낼 수 있게 된다.

$k$가 행렬의 행 순서 $j$가 행렬의 열 순서가 된다.(0부터 시작) 또한 행렬의 각 성분은 $w_n^{jk}$로 나타난다.


각 데이터점이 여러 진동수로 분해되어 더해짐 푸리에 변환과 역변환이 쌍을 이루어 부호만 반전되어 나타나는 것처럼 DFT의 역변환도 유사하게 나타난다.
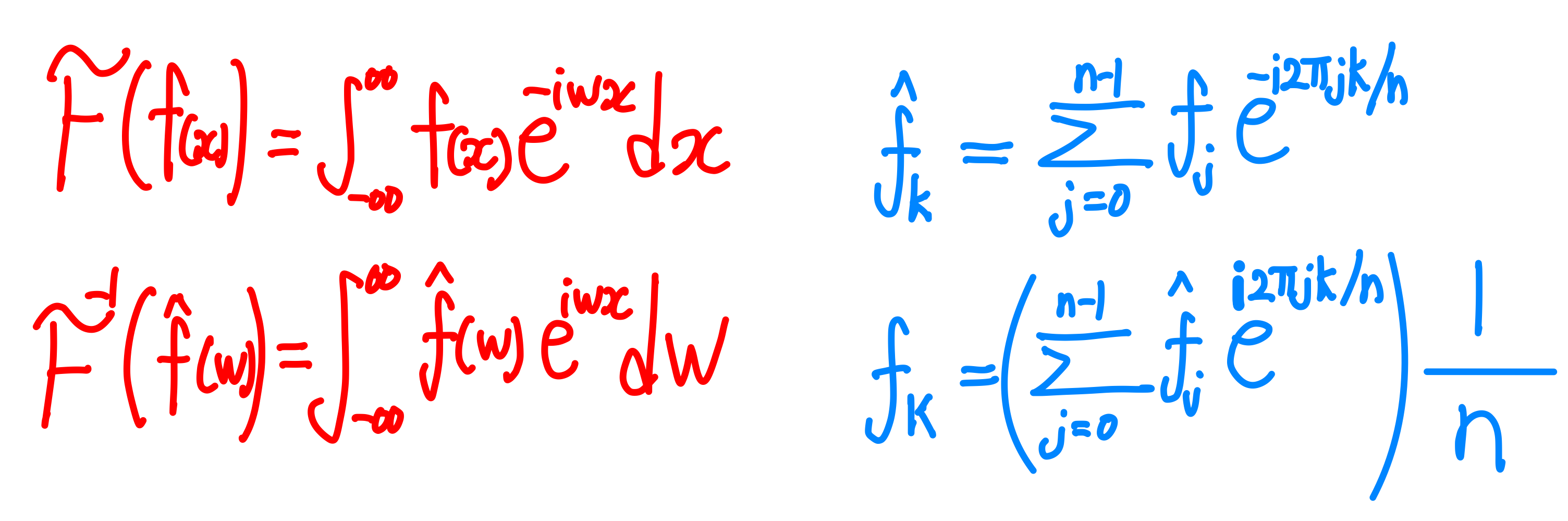
'Math♾️ > Fourier Analysis' 카테고리의 다른 글
FFT를 이용한 noise 제거하기 (3) 2022.09.17 Fast Fourier Transform (FFT) (0) 2022.09.17 푸리에 변환의 선형성과 Parseval's Theorem (0) 2022.09.06 합성 곱과 푸리에 변환 (0) 2022.09.06 The Fourier Transform and Derivatives (0) 2022.09.06