-
Fast Fourier Transform (FFT)Math♾️/Fourier Analysis 2022. 9. 17. 00:35
FFT
이산 푸리에 변환은 데이터들이 이산적인 형태로 주어졌을 때 이를 벡터로 나타내어 각 데이터점이 어떠한 진동수들로 구성되어 있는지 푸리에 변환을 통해 쪼개고 같은 진동수끼리 합하여 전체 데이터들이 어떠한 진동수를 가지고 있는지 푸리에 domain에서 나타내는 방법이다.

이산 푸리에 변환(DFT)를 이용할 경우에는 $n$개의 $f_n$이 $w^{jk}$ 행렬의 각 행에서 $n$번 곱을 수행하며 이런한 연산을 모든 $n$개의 행에 대해서 반복적으로 수행하므로 빅오 표기법으로 나타내면 DFT 알고리즘의 계산 복잡도는 $O(N^2)$이다.
$O(N^2)$의 경우 주어진 데이터의 개수가 늘어날 때 연산 횟수가 제곱에 비례하여 늘어나므로 연산에 필요한 자원이 엄청나다.
따라서 DFT는 데이터의 개수가 조금만 늘어나도 연산이 어려움을 겪으므로 DFT와 똑같은 output을 갖으면서도 연산의 양을 줄일 수 있는 방법이 필요하다.
각 데이터점 $f$를 푸리에 변환하는 $w^{jk}$행렬을 조작하여
좀 더 효율적인 연산이 가능토록 하는 알고리즘이 Fast Fourier Transform (FFT) 이다.
FFT 알고리즘의 계산 복잡도는 $O(n*log(n))$이므로 데이터 개수가 늘어날수록 DFT에 비하여 훨씬 빠른 연산이 가능하다.
대략적인 방법을 살펴보면 다음과 같다.

데이터가 1024개 주어졌을 때 $w^{jk}$의 크기는 1024*1024이다.

행렬의 개수가 늘어나 연산이 늘어난 것처럼 보이지만 행렬의 성분들을 잘 살펴보면 연산이 간단한 단위 행렬과 대각 행렬로 바뀌었다.
위와 같은 행렬의 변환 과정을 반복적으로 수행하면 연산의 크기가 확연히 줄어들어 효율적인 계산이 가능해진다.
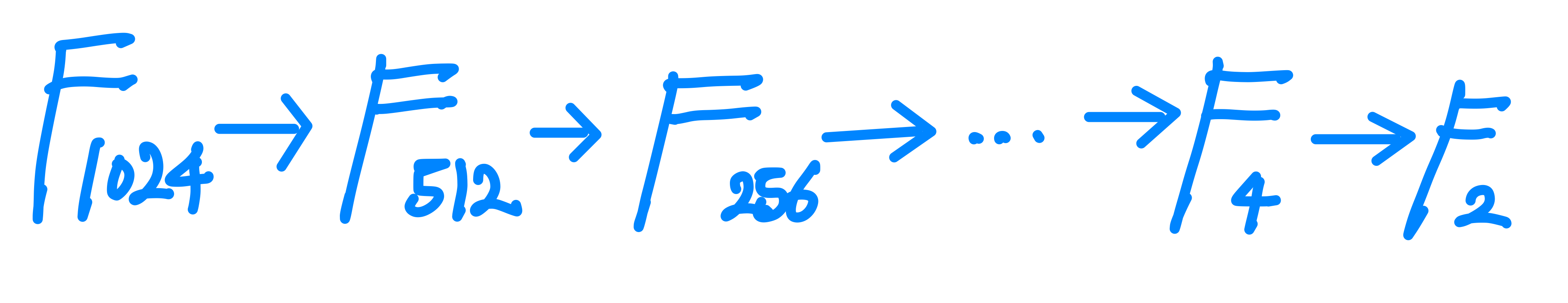
'Math♾️ > Fourier Analysis' 카테고리의 다른 글
FFT를 이용한 미분값 계산 (0) 2022.09.19 FFT를 이용한 noise 제거하기 (3) 2022.09.17 Discrete Fourier Transform (DFT) (1) 2022.09.15 푸리에 변환의 선형성과 Parseval's Theorem (0) 2022.09.06 합성 곱과 푸리에 변환 (0) 2022.09.06