FFT를 이용한 미분값 계산

푸리에 변환과 미분

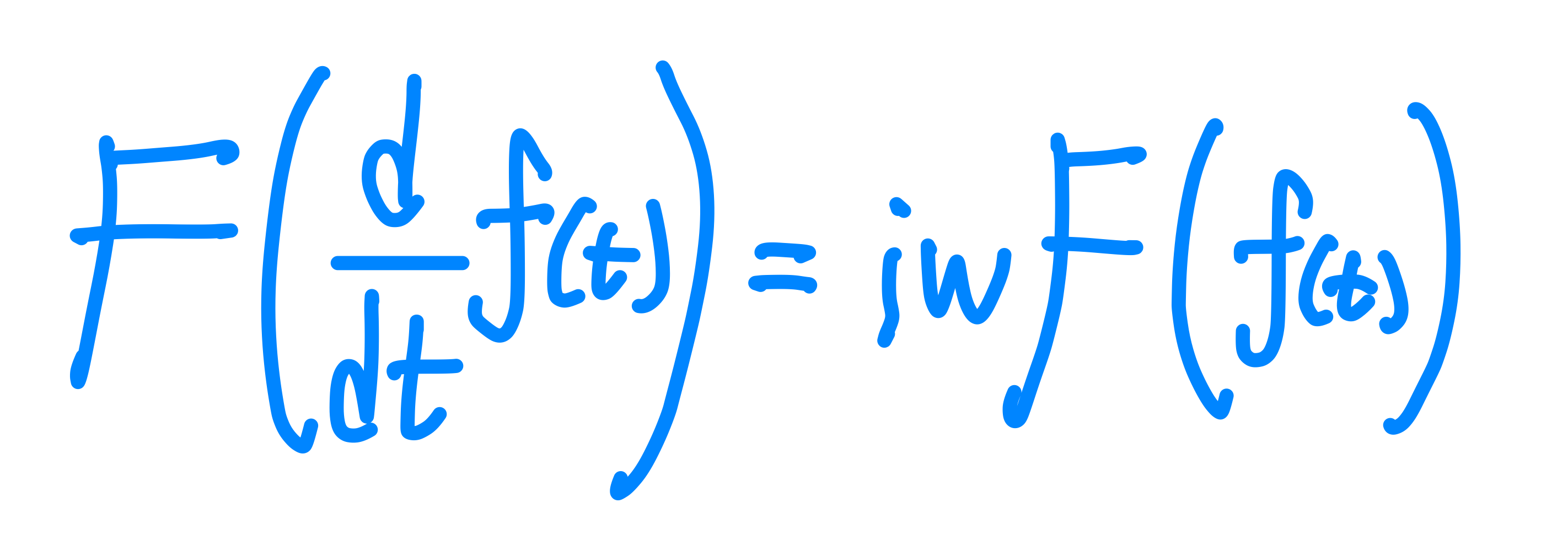
$f(t)$의 미분형을 푸리에 변환하게 되면 위와 같이 $iw$ 텀과 $f(t)$의 푸리에 변환으로 나타나는 것을 알 수 있다. 

즉 $f(t)$를 푸리에 변환한 이후 $iw$을 곱한것을 푸리에 역변환하게 되면 $f(t)$의 미분형을 얻을 수 있다.

 

푸리에 변환시 미분 특징을 FFT에 이용

FFT는 DFT 연산을 빠르게 하는 방법으로 이산적인 데이터에 대하여 푸리에 변환을 가능하게 한다.

푸리에 변환시 미분의 특징을 이산적인 데이터에 적용하면 다음과 같이 나타난다. 

그림에서 $k$는 $w$와 동일한 역할을 한다. 

- $w$는 시간 텀에 대하여 미분하였을 때 사용하며 temporl frequency라고 한다.

- $k$는 공간 텀에 대하여 미분하였을 때 사용하며 spatial frequency 또는 wave number라고 한다. 

 

위의 관계를 이용하여 이산적 데이터 $f$의 미분 값을 구할 수 있다.

각 $f$에 대하여 푸리에 변환을 한 값에 대응하는 $k$와 i를 곱한 것의 푸리에 역변환을 하면 된다.

 

 

- 해석적으로 미분형을 구할 수 있는 경우를 예로 들어 FFT를 이용해 구한 미분값이 얼마나 근사한지 알아본다. 

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [12, 12]
plt.rcParams.update({'font.size': 18})

# 해석적으로 구한 미분값

n = 128                                                    # x
L = 30                                                     # 주기 30
dx = L/n                                                   # delta x
x = np.arange(-L/2,L/2,dx,dtype='complex_')                # 정의역 x -15~15
f = np.cos(x) * np.exp(-np.power(x,2)/25)                  # 함수 f
df = -(np.sin(x) * np.exp(-np.power(x,2)/25) + (2/25)*x*f) # 함수 f의 미분

 

- 전방차분법을 이용하여 미분값을 구하여 FFT를 이용하여 미분값을 구한 경우와 비교해본다.

# 전방차분법을 이용한 미분값 계산

dfFD = np.zeros(len(df),dtype='complex_')   # 전방차분법으로 구한 미분형들이 들어갈 공간 마련

for kappa in range(len(df)-1):              # f(x+dx)-f(x)/dx를 이용
    dfFD[kappa] = (f[kappa+1]-f[kappa])/dx  # 각 x에서의 미분값 구하기 
    
dfFD[-1] = dfFD[-2]                         # 전방차분법 이용하였으므로 마지막 항은 뒤에서 두번째

 

- FFT를 이용하여 미분값 구하는 방법

# FFT를 이용한 미분값 계산

fhat = np.fft.fft(f)                    # 각 f를 FFT로 푸리에 변환
kappa = (2*np.pi/L)*np.arange(-n/2,n/2) # 2pi/L *(-n/2~n/2)로 kappa(wave number)로 구하기 
kappa = np.fft.fftshift(kappa)          # fft 진동수에 맞게 kappa 재정렬
dfhat = kappa * fhat * (1j)             # F(df/dt) = i*k*fft
dfFFT = np.real(np.fft.ifft(dfhat))     # df/dt = F^{-1}(i*k*fft)

 

- 그래프로 나타내기

plt.plot(x,df.real,color='k',linewidth=2,label='True Derivative')
plt.plot(x,dfFD.real,'--',color='b',linewidth=1.5,label='Finite Diff.')
plt.plot(x,dfFFT.real,'--',color='r',linewidth=1.5,label='FFT Derivative')
plt.legend()
plt.show()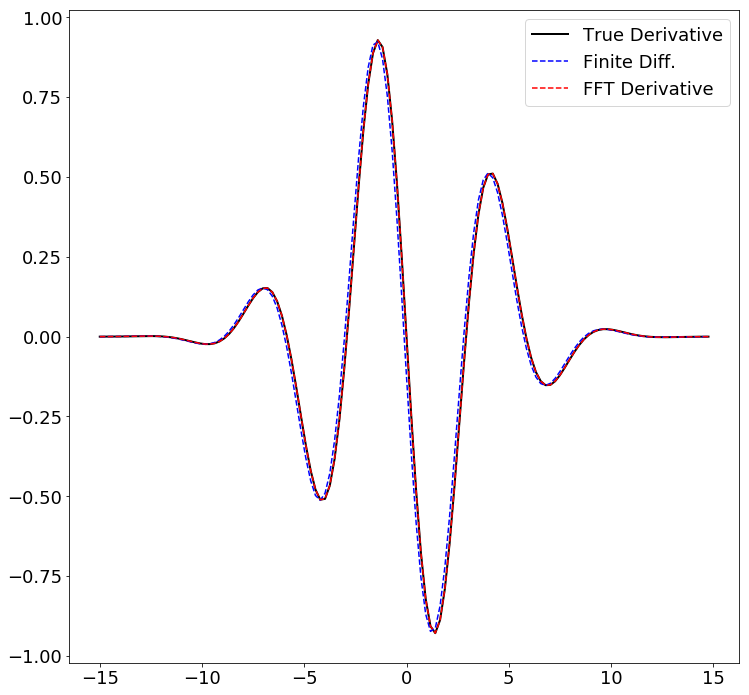

 

 

해석적으로 구한 미분값이 검은색 실선, 유한차분법을 이용한 것이 파란색 점선, FFT를 이용한 것은 빨간색 점선으로 나타내었다.

그림을 보면 빨간색 점선이 검은색 실선 상에 위치하고 있다. 따라서 FFT를 이용하여 구한 미분값은 해석적으로 구할 때와 거의 일치한다.

그에 비해 파란색 점선은 완전히 일치하지는 않는다. 그러므로 FFT를 이용할 때 유한차분법에 비해 효과적으로 미분값을 구할 수 있다.

---