FFT를 이용한 PDE 풀이

Heat Equation (1D)

위의 방정식은 1차원에서의 시간과 위치(x)에 따른 열분포의 변화를 나타내는 편미분방정식이다. 

온도 $u$가 시간 $t$와 공간 $t$에 대하여 변화하므로 두가지 변수에 대한 변화를 동시에 고려해야하므로 해를 구하기가 어렵다. 

 

이때 공간 $x$에 대하여 푸리에 변환을 취하게 되면 $x$를 $k$로 상수의 형태로 바뀌므로 시간과 공간에 대한 편미분 방정식이 오로지

시간에만 대한 상미분 방정식으로 바뀌게 된다. 따라서 해를 구하기에 용이해진다.

 

미분 텀에 대하여 푸리에 변환을 하게 되면 아래와 같은 형태로 나타난다.

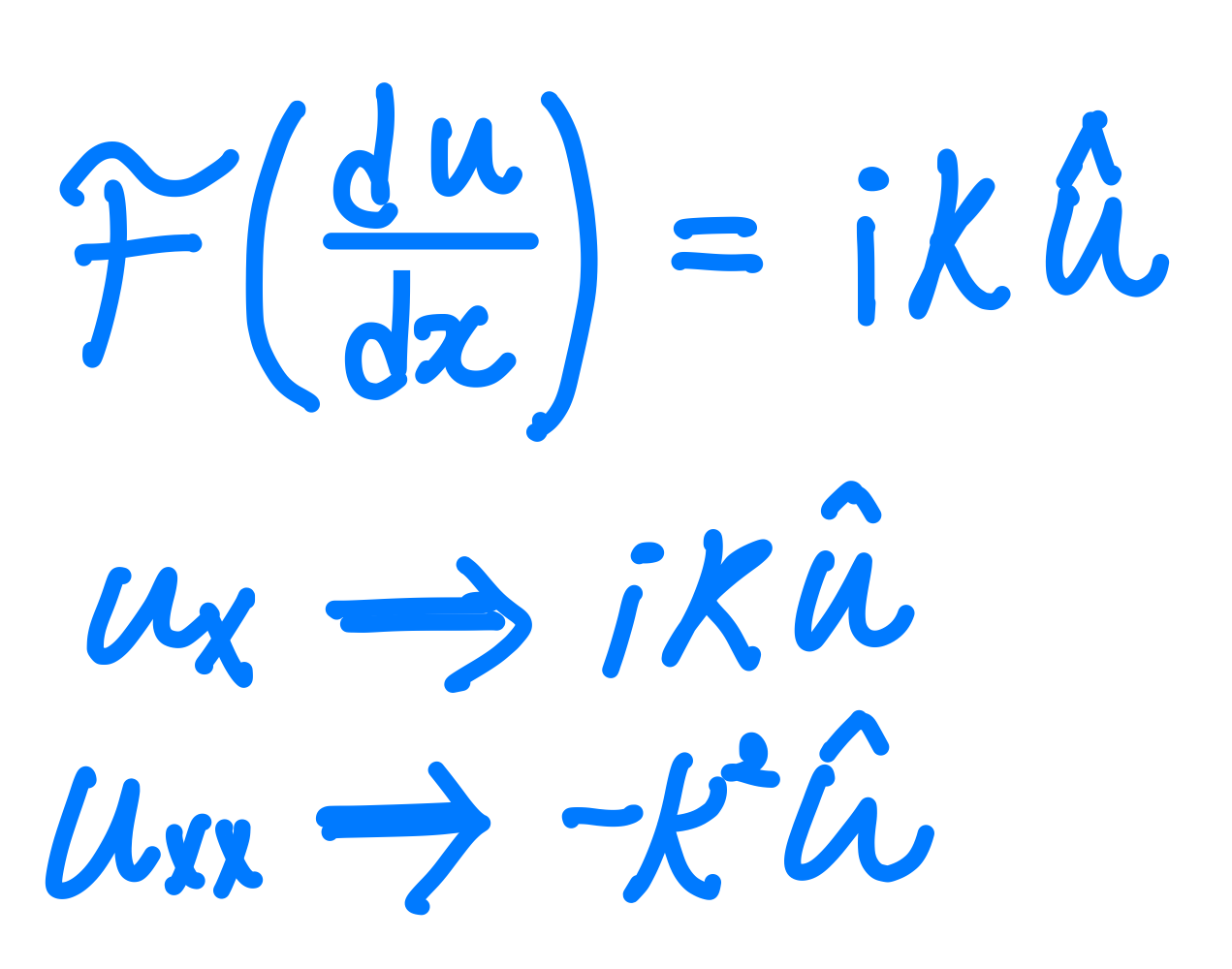
따라서 편미분 방정식을 푸리에 변환하게 되면 다음과 같이 바뀌게 된다. 

이산적인 데이터에 대하여 FFT를 이용하여 계산할 때는 공간 term에 대한 푸리에 변환이 아래와 같이 벡터의 형태로 주어진다. 

따라서 각 $k_j$에 대해 분리된($k$가 서로 영향을 주지 않음) $n$개의 상미분 방정식의 형태로 나타난다. 

 

- 해 도출 과정

1. 편미분 방정식을 공간 term에 대하여 푸리에 변환하여 시간에 대한 상미분 방정식으로 만들기 (고려할 변수 2개에서 1로 만들기)

2. 상미분 방정식을 적분을 이용하여 해 도출하기

3. 도출한 해를 푸리에 역변환하여 원래의 x,t 좌표계에서 나타내기

 

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import axes3d
plt.rcParams['figure.figsize'] = [12, 12]
plt.rcParams.update({'font.size': 18})


# 열미분방정식(1D)풀이 
# 각 위치에서 온도가 주어졌을 때 시간이 지남에 따라 각 위치에서 온도가 어떻게 변화하는가?
# 방정식의 해 => u(x,t) = ? (시간과 위치를 해에 대입하면 해당 시간과 위치에서의 온도가 나온다.)

# 정의역 설정(x)
a = 1                      # 열전도율
L = 100                    # 주기
N = 1000                   # 주기내에 이산적으로 나타날 데이터점 개수
dx = L/N                   # 각 데이터간의 간격
x = np.arange(-L/2,L/2,dx) # 정의역 설정

# 이산데이터에 대한 wavenumbers 정의 
kappa = 2*np.pi*np.fft.fftfreq(N, d=dx)

# 초기상태의 열분포 (모자모양)
u0 = np.zeros_like(x)                     
u0[int((L/2 - L/10)/dx):int((L/2 + L/10)/dx)] = 1
u0hat = np.fft.fft(u0) 

# SciPy의 odeint 함수는 복소수에서의 계산이 어려우므로 N개의 복소수 벡터를 2N개의 실수 벡터로 다룬다.
u0hat_ri = np.concatenate((u0hat.real,u0hat.imag))

# 정의역 설정(t)
dt = 0.1
t = np.arange(0,10,dt)

# 위에서 주어진 시간 t, wavenumber kappa, 열전도율 a, 공간에 대한 푸리에 변환값을 이용
# 푸리에 변환된 열방정식을 구성하는 함수
def rhsHeat(uhat_ri,t,kappa,a):
    uhat = uhat_ri[:N] + (1j) * uhat_ri[N:]
    d_uhat = -a**2 * (np.power(kappa,2)) * uhat
    d_uhat_ri = np.concatenate((d_uhat.real,d_uhat.imag)).astype('float64')
    return d_uhat_ri

# 푸리에 변환된 방정식 적분하여 해를 구함
uhat_ri = odeint(rhsHeat, u0hat_ri, t, args=(kappa,a))
uhat = uhat_ri[:,:N] + (1j) * uhat_ri[:,N:]
u = np.zeros_like(uhat)

# 구한 해를 푸리에 역변환하여 원래의 x,t좌표에서 나타냄
for k in range(len(t)):
    u[k,:] = np.fft.ifft(uhat[k,:])
u = u.real    

# 구한 해를 3d로 plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

u_plot = u[0:-1:10,:]
for j in range(u_plot.shape[0]):
    ys = j*np.ones(u_plot.shape[1])
    ax.plot(x,ys,u_plot[j,:])
    
# 구한 해를 이미지로 plot
plt.figure()
plt.imshow(np.flipud(u), aspect=8)
plt.axis('off')
plt.show()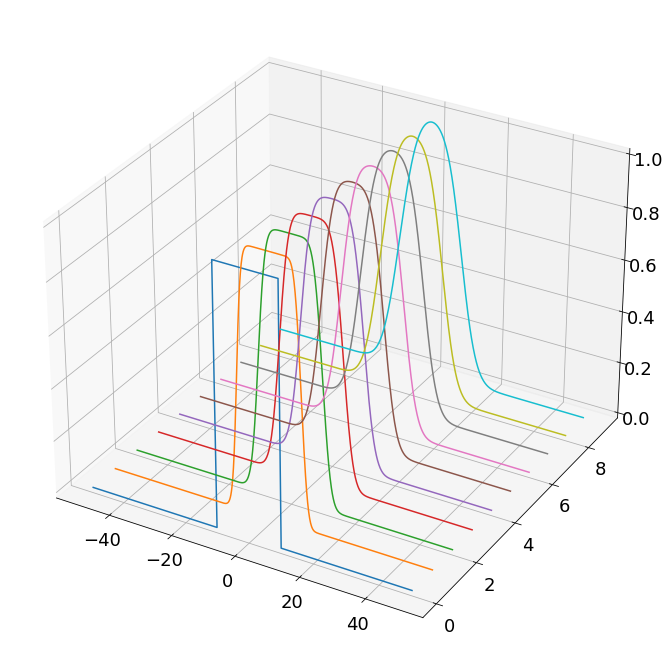

도출한 해에 값을 대입하였을 때 나타나는 모습

위의 그림에서 왼쪽아래 축이 x(위치)축이며 오른쪽 아래가 t(시간)축이다. 또한 오른쪽 위가 u(온도)축이다.

시간이 흐름에 따라 위치별 온도의 변화를 나타내며 제일 앞에 있는 파란색 그래프가 초기값으로 구성한 처음 온도의 상태이다.

모서리의 뾰족한 부분이 먼저 부드럽게 변하면서 점점 가우시안 분포의 형태로 온도가 변화하는 것을 알 수 있다.

 

푸리에 변환이 뭔 짓을 한것일까?

왜 푸리에 변환을 하면 미분 term이 상수값으로 바뀌어 나타나는 것일까?

 

- 고유벡터와 고윳값에 대하여

 

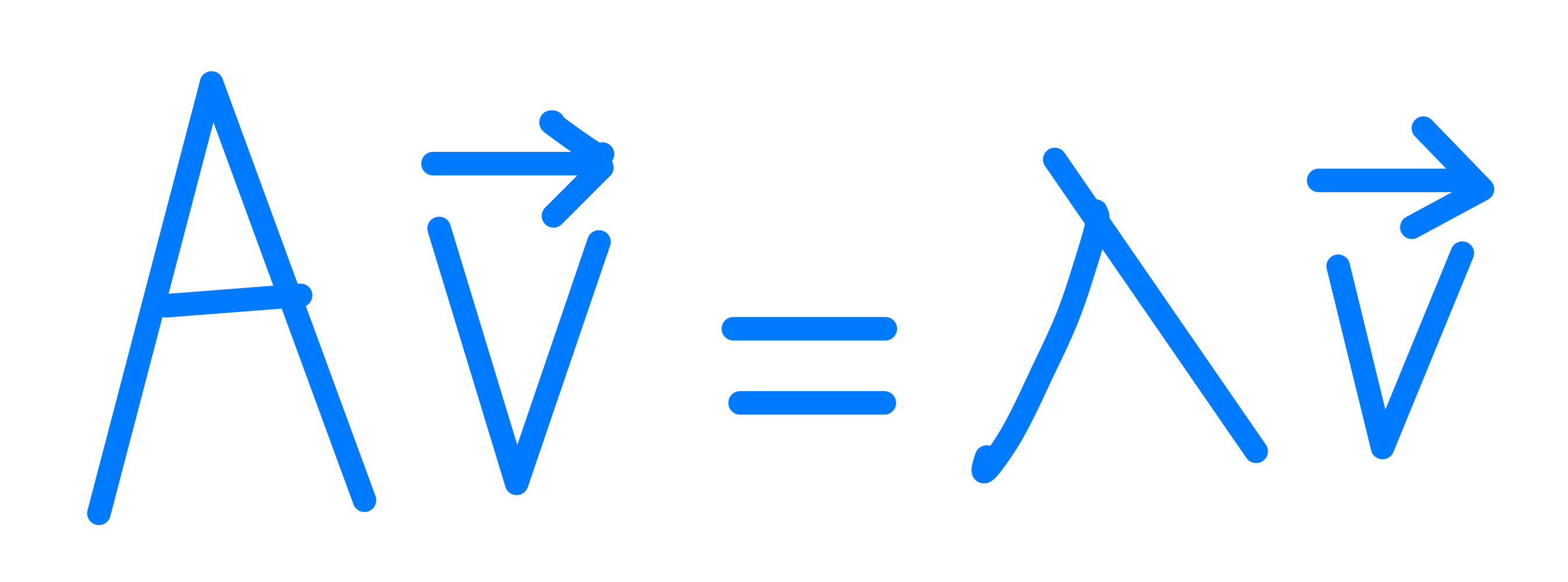
위는 행렬 $A$, 고유벡터 $\vec{v}$, 고윳값 $\lambda$ 간의 관계를 나타내는 식이다. 위 식은 무엇을 의미할까?

 

고유벡터 $\vec{v}$에 행렬을 곱하였더니 방향은 $\vec{v}$을 유지하며 벡터의 크기만 $\lambda$만큼 변화하였다.

 

"고유벡터는 행렬이 곱해졌을 때 방향이 변하지 않는다" 이것이 고유벡터가 변화를 나타낼 때 유용하게 쓰이는 이유이다. 

 

고유벡터가 아닌 벡터들은 행렬 곱으로 인한 변화가 방향과 크기 모두 일어나게 된다.

따라서 서로 선형독립인 벡터들을 기저로 하는 좌표계를 사용하더라도 고유벡터가 아닐 경우

행렬 곱으로 인한 변환이 각 기저벡터들의 방향을 변화시켜 각 축간의 중첩이 생겨 선형독립이 깨지게 되며

해당 좌표계상에서 나타나던 값들이 행렬로 인해 어떻게 변화하였는지 알기가 어렵게 된다. 

 

고유벡터의 경우에는 행렬 곱으로 인한 변화가 크기로만 나타난다. 

행렬 곱으로 인한 변환에도 각 기저들은 방향을 유지하기 때문에 축간의 독립성이 유지되어 좌표계상에서 나타나던 값들의 변화를 파악하기 용이한 형태가 된다. 

 

행렬 A의 고유벡터 $\vec{v}$를 기저로 하는 좌표계는 행렬 A곱으로 인한 변화가 각 기저의 $\lambda$만큼의 상수배(각 축의 신장) 형태로 나타난다. 

 

이러한 관계를 이용하여 임의의 행렬 A로 인해 변화가 생길 때

1. 원래 좌표계의 기저벡터 $\vec{x}$를 행렬 A의 고유벡터 $\vec{v}$로 바꾸는 좌표변환을 한다.

2. 변환된 좌표상에서 행렬 A로 인한 변화를 고유벡터의 상수배 형태로 나타낸다.

3. 상수배된 고유벡터를 다시 원래 좌표계를 이루던 기저벡터로 되돌린다.

 

변화가 일어나는 방향을 가지고 있는 기저벡터들로 구성된 좌표로 좌표변환을 하게 되면 변화가 단순 상수배 형태로 나타난다. 

 

- 푸리에 변환도 좌표변환이다. 

 

열방정식에서 $x$축에 대하여 푸리에 변환을 하게 되면 x방향에 대한 변화(미분)가 단순 상수($k^2$)으로 바뀌는 것도 

행렬 A에 의한 변화 방향을 나타내는 고유벡터로 좌표를 변환하는 것과 같이 

$x$ 미분에 의한 변화 방향을 가리키는 고유벡터로 좌표를 변환하는 것이다. 

 

변화에 대하여 변화의 방향을 나타내는 방법이 존재한다면 변화를 간단히 나타낼 수 있게 된다.

 

어떠한 현상을 관측하였는데 해당 현상이 영향을 받는 변수가 두가지 이상인 경우 

나타나는 현상과 각 변수간의 관계를 분석하는데 어려움을 겪기 때문에

현상을 구성하는 변수에 대하여 푸리에 변환을 하면(좌표계를 바꾸면)

바뀐 좌표계에서는 푸리에 변환한 변수에 의한 변화는 상수배의 형태로 나타낼 수 있기 때문에

편미분방정식에 푸리에 변환을 하여 해를 찾은 이후 다시 푸리에 역변환을 통해 원래의 좌표계에 대하여 찾은 해를 표현하는 것이다. 

---