-
Gibbs PhenomenaMath♾️/Fourier Analysis 2022. 9. 2. 23:19
Gibbs Phenomena

위와 같이 함수에 급격하게 값이 뛰는 점이 존재할 때 이를 불연속 점이라고 한다.
불연속점이 존재하는 함수를 푸리에 급수로 나타내게 되면 아래와 같이 나타난다.

불연속점이 존재하는 근방에서 푸리에 급수를 통해 근사시킨 값들이 진동하는 것을 알 수 있다.
이러한 현상을 깁스 현상이라고 한다.
임의의 주기함수를 푸리에 급수를 이용해 각 진동수 $k$로 분해할 때 진동수 $k$의 파형은 $cos(kx)$과 $sin(kx)$를 기저로 하여 구성되게 된다. 이때 $cos(kx),sin(kx)$ 모두 연속 함수이기 때문에 이들을 결합하여 값이 급격하게 변화하는 불연속 값을 나타내기 어렵다.
파이썬을 이용하여 나타낸 gibbs 현상
import numpy as np import matplotlib.pyplot as plt plt.rcParams['figure.figsize'] = [8, 8] plt.rcParams.update({'font.size': 18}) dx = 0.01 L = 2 * np.pi x = np.arange(0, L + dx, dx) n = len(x) nquart = int(np.floor(n/4)) f = np.zeros_like(x) f[nquart:3*nquart] = 1 A0 = np.sum(f * np.ones_like(x)) * dx * 2/L fFS = A0/2 * np.ones_like(f) for k in range(1, 101): Ak = np.sum(f*np.cos(2*np.pi*k*x/L)) * dx * 2/L Bk = np.sum(f*np.sin(2*np.pi*k*x/L)) * dx * 2/L fFS = fFS + Ak*np.cos(2*np.pi*k*x/L) + Bk*np.sin(2*np.pi*k*x/L) fig, axs = plt.subplots(3, 1) axs[0].plot(x, f, color='r') plt.sca(axs[0]) plt.title('f(x)') axs[1].plot(x, fFS, color='b') plt.sca(axs[1]) plt.title('Fourier series') axs[2].plot(x, f, color ='r', linewidth = 2) axs[2].plot(x, fFS, color ='b',linewidth =1) plt.sca(axs[2]) plt.title('Overlap') plt.subplots_adjust(left=0.125, bottom=0.1, right=0.9, top=0.9, wspace=0.2, hspace=0.5)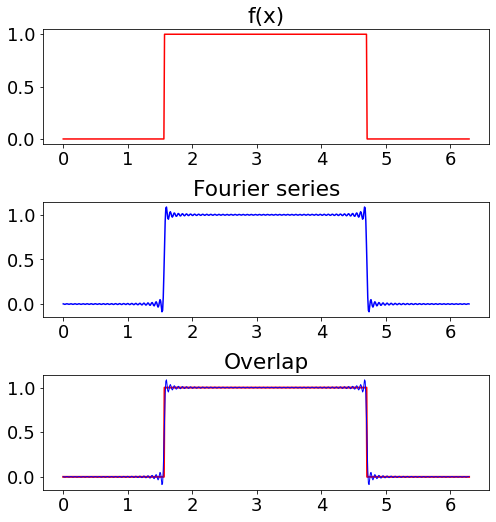
import numpy as np import matplotlib.pyplot as plt from matplotlib import animation, rc from IPython.display import HTML plt.rcParams['figure.figsize'] = [8, 8] plt.rcParams.update({'font.size': 18}) plt.rcParams['animation.html'] = 'jshtml' dx = 0.01 L = 10 x = np.arange(0,L+dx,dx) n = len(x) nquart = int(np.floor(n/4)) f = np.zeros_like(x) f[nquart:3*nquart] = 1 A0 = np.sum(f * np.ones_like(x)) * dx * 2 / L fFS = A0/2 * np.ones_like(f) fig,ax = plt.subplots() plt.plot(x,f,color='k',linewidth=2) fFS_plot, = plt.plot([],[],color='r',linewidth=2) all_fFS = np.zeros((len(fFS),101)) all_fFS[:,0] = fFS for k in range(1,101): Ak = np.sum(f * np.cos(2*np.pi*k*x/L)) * dx * 2 / L Bk = np.sum(f * np.sin(2*np.pi*k*x/L)) * dx * 2 / L fFS = fFS + Ak*np.cos(2*k*np.pi*x/L) + Bk*np.sin(2*k*np.pi*x/L) all_fFS[:,k] = fFS def init(): ax.set_xlim(x[0],x[-1]) ax.set_ylim(-0.2, 1.2) return fFS def animate(iter): fFS_plot.set_data(x,all_fFS[:,iter]) return fFS_plot anim = animation.FuncAnimation(fig,animate,init_func=init,frames=101,interval=50,blit=False,repeat=False) HTML(anim.to_jshtml())
k : 1 ~ 101 
k : 1 ~ 315 'Math♾️ > Fourier Analysis' 카테고리의 다른 글
The Fourier Transform and Derivatives (0) 2022.09.06 푸리에 변환에 대하여 (0) 2022.09.05 푸리에 급수/ 파이썬으로 확인하기 (0) 2022.09.02 복소수 공간에서의 푸리에 급수 (0) 2022.06.20 함수간의 내적에 대하여 생각하기 (2) 2022.05.20