-
완비정보하의 정태적 게임Game Theory 2022. 4. 15. 14:35
완비정보: 게임에서 플레이어들의 보수구조를 모두 알고 있는 상태
정태적게임: 상대방의 선택을 모르는 상태에서 진행하는 게임
-> 게임의 보수구조는 알고 있지만 각 경기자들이 상대방의 선택을 모르는 채로 의사결정을 해야하는 게임상황
우월전략균형
1. 강우월 (s strictly dominates s')
경기자 2의 어떤 전략 $s_2$에 대해서도 $u_1(s,s_2)>u_1(s',s_2)$가 성립하면 경기자 1에게 전략$s$는 $s'$에 대해 강우월하다고 한다.
-> 상대가 가진 모든 전략에 대하여 내가 가진 전략 s가 s'보다 좋은 상황을 의미한다. (상대적인 의미)
이 상황에서는 경기자 1은 반드시 s'보다는 s를 선택하는 것이 합리적이다.
이때 전략s'은 s에 대하여 강열등(strictly dominated)하다고 한다.
2. 강우월전략(dominant strategy)
경기자 1의 전략 $s^*$가 자신의 다른 모든 전략 $s_1$에 대해 강우월하면 전략 $s^*$를 1의 강우월전략이라고 한다.
즉 모든 $s_2\in S_2$와 $s_1\ne s^*$인 모든 $s_1\in S_1$에 대해 $u_1(s^*,s_2)>u_1(s_1,s_2)$가 성립하면 $s^*$는 경기자 1에게 강우월전략이라고 한다.
-> 상대가 가진 모든 전략에 대하여 나의 전략 $s^*$가 내가 가진 다른 전략들보다 좋은 상황이다. (절대적인 의미)
만약 경기자에게 강우월전략이 존재한다면 반드시 선택하게 된다. 왜냐하면 정의상 다른사람들의 선택에 관계없이 항상 자신의 다른 어떠한 전략보다 더 높은 보수를 가져다 주는 전략이기 때문이다.
※죄수의 딜레마

죄수의 딜레마 - 범인1의 입장
상대가 자백 했을때 자백은 2, 부인은 0으로 자백이 유리
상대가 부인 했을때 자백은 4, 부인은 3으로 자백이 유리
따라서 범인 1에게 자백은 상대의 선택과 관계없이 자신의 전략집합중 가장 좋은 강우월전략이다.
- 범인2의 입장
상대가 자백했을때 자백은 2, 부인은 0으로 자백이 유리
상대가 부인했을때 자백은 4, 부인은 3으로 자백이 유리
따라서 범인 2에게도 자백은 상대의 선택과 관계없이 자신의 전략집합중 가장좋은 강우월전략이다.
(강)우월전략균형
- 위의 상황에서 각 범인들은 모두 자백이 강우월전략이므로 합리적이라면 이를 선택할것이다. 이때의 전략명세 (자백,자백)을
우월전략 균형이라고 한다.
- 상대방의 전략을 고려할 필요가 없으므로(강우월전략이 존재하므로) 사실상 비전략적 상황이다.
- 따라서 상대의 합리성에 대한 가정도 필요하지 않다.(상대를 고려하지 않으므로)
- 각 범인들은 강우월전략을 선택하여서 보수(2,2)을 받게 되지만 보수행렬을 보면 (3,3) 모두 부인경우가 효용이 제일크다.
-> 개인의 합리성이 사회적 합리성및 효율성을 담보하지 않는 점이 나타난다.
3. 약우월(s weakly dominates s')
경기자 2의 모든 전략 $s_2$에 대해서 $u_1(s,s_2)\ge u_1(s',s_2)$가 성립하고 경기자 2의 어떤 전략 $s'_2$ 에 대해서는
$u_1(s,s'_2)> u_1(s',s'_2)$이 성립하면, 전략 $s$는 $s'$에 대해 약우월하다고 한다.
-> 상대방의 모든전략에 대해 s가 s'보다 같거나 더 좋으면서, 상대방의 어떤 특정 전략에 대해서는 s가 s'보다 좋은 상황이다.
경기자가 s'대신 s를 택함으로서 손해는 보지 않는다.
4. 약우월전략(weakly dominant strategy)
경기자 1의 전략 $s^*$이 자신의 다른 모든 전략에 대해 약우월하면 $s^*$는 1의 약우월전략이라고 한다.
즉 모든 $s_2\in S_2$와 $s_1\ne s^*$인 모든 $s_1\in S_1$에 대해 $u_1(s^*,s_2)\ge u_1(s_1,s_2)$가 성립하고,
어떤 $s'_2$에 대해서 $u_1(s^*,s'_2)>u_1(s_1,s'_2)$이 성립하면, 전략 $s^*$는 1에게 약우월전략이다.
-> 상대가 가진 모든 전략에 대해 $s^*$가 나의 다른 전략들보다 좋거나 같으며 상대방의 특정전략에 대해서는 나의 전략중 가장 좋은
전략일 경우 약우월전략이라고 한다.
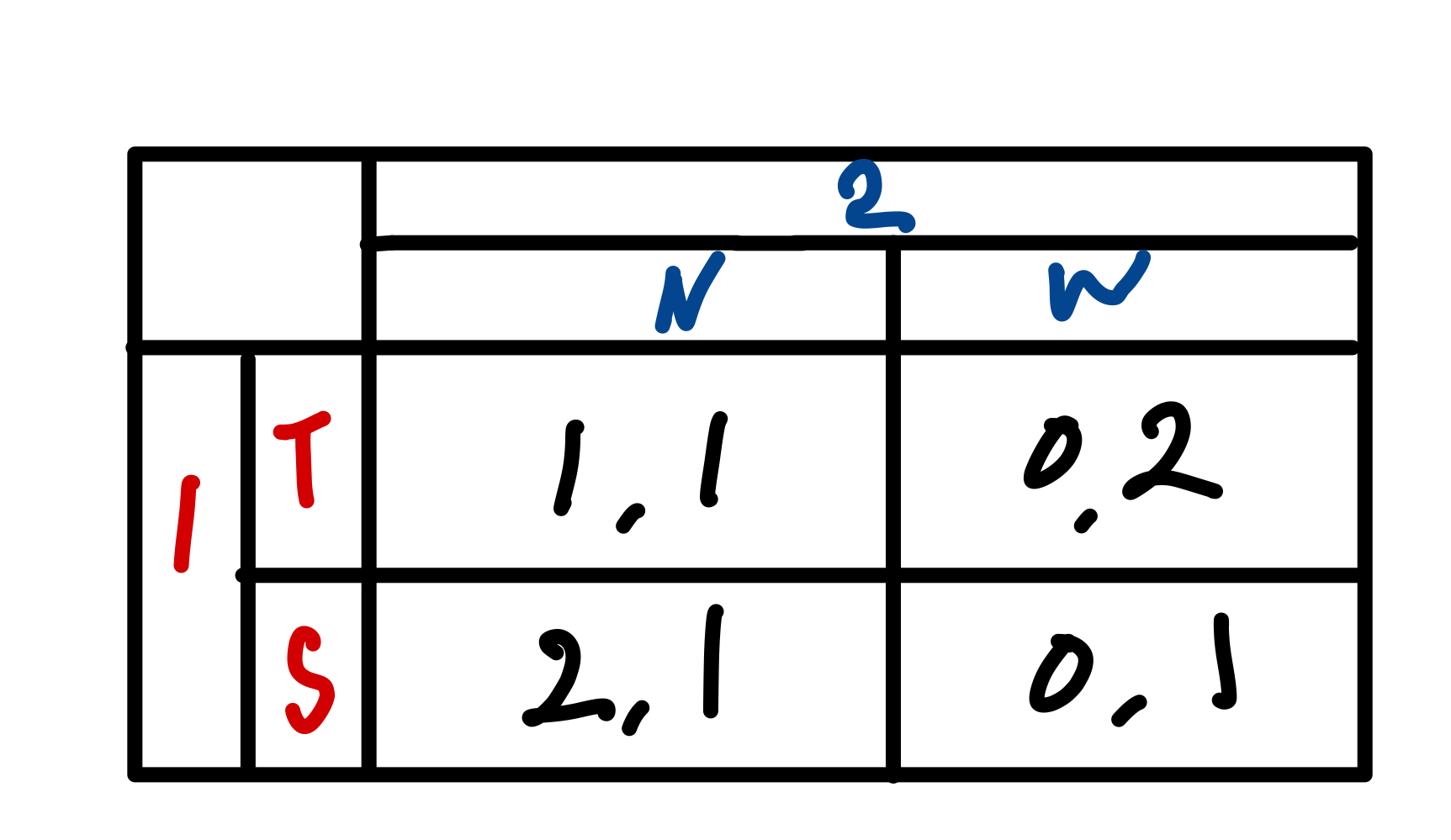
약우월 전략 - 경기자 1의 입장
경기자 2가 W을 선택한 경우 경기자 1에게 T나 S는 똑같은 보수를 주므로 차이가 없다(상대방의 전략에 대해서 같거나)
경기자 2가 N을 선택한 경우 경기자 1에게 S는 T보다 더 큰 보수를 준다(상대방의 특정전략에 대해서는 내 전략중 가장 좋은 전략)
=> 따라서 경기자 2에게 N은 약우월전략이다.
강열등전략의 반복적제거(Iterated Deletion of Strictly Dominated Strategy)
각 경기자들이 합리성을 지니고 있기 때문에 각자의 강열등전략은 선택하지 않을 것이라는 믿음가지고 각 경기자들의 강열등전략을
순차적,반복적으로 제거하여 게임의 가능한 결과(전략명세)를 축소시키는 과정을 말한다.

IDSDS 1. 경기자 1에게 전략b는 d에 대해 강열등하므로 전략b를 제거한다.
2,3. 경기자 2는 경기자1이 전략b를 제거할것을 알고 있다. 이때 전략g는 전략h에 대해 강열등하므로 전략g를 제거한다.
또한 전략f도 전략 h에 대해 강열등하므로 전략f도 제거한다.
4. 경기자 1은 경기자2가 전략 f,g를 제거할것을 알고 있다. 이때 전략a는 전략d에 대해 강열등하므로 전략a를 제거한다.
결과적으로 경기자 1에게 남은 전략집합은 c,d이며 경기자2에게 남은 전략집한은 e,h로 가능한 전략명세가 축소됨을 알 수 있다.
'Game Theory' 카테고리의 다른 글
내쉬균형의 응용 - 공유지의 비극 (0) 2022.04.19 내쉬균형의 응용 - 베르트랑 모형(Bertrand Model) (0) 2022.04.19 내쉬균형의 응용 - 쿠르노 모형 (0) 2022.04.18 내쉬균형(Nash Equilibrium) (1) 2022.04.15 게임이론의 정의 (0) 2022.04.15