선형 변환 : 행렬은 함수다.

선형 변환이란 무엇인가? 

먼저 '변환(transformation)'라는 용어부터 이해해볼까요? 변환은 사실 함수(function)의 또 다른 표현일 뿐입니다. 

함수는 입력 값과 출력 값간의 관계를 정의합니다. 따라서 임의의 입력 값이 주어졌을 때 정의된 관계에 따라 출력값이 결정됩니다. 

선형 대수학에서는 특히 주어진 입력 값과 출력값이 '벡터'인 경우를 주로 다룹니다. 

 

그렇다면 왜 함수 대신 변환이라는 용어를 사용하였을까요? 

이는 입력 벡터와 출력 벡터간의 관계를 시각적으로 '움직임'으로써 이해하도록 유도하기 위함입니다. 

즉, 입력 벡터가 출력 벡터로 '이동'한다고 생각하는 것이죠. 

선형 변환의 조건 

변환이 '선형'이 되기 위해서는 다음 조건을 만족해야합니다. 

첫번째로, 모든 직선은 직선으로 유지되어야합니다. (곡선이 되서는 안 됨)

두번째로, 원점(0,0)의 위치는 고정되어야합니다. 

 

예를 들어 좌표 격자를 이루는 직선이 곡선이 되거나 원점이 다른 곳으로 이동하는 경우 해당 변환은 선형이 아닙니다.

따라서 일반적으로 선형 변환은 격자선들이 서로 평행하고 균등한 간격으로 유지합니다. 

기저 벡터만 봐 

Span(기저 벡터들의 선형결합)으로 만들어진 공간상에는 무한한 벡터들이 존재합니다. 

그러면 어떻게 이 수 많은 벡터들이 선형 변환시 어디로 이동할지를 알 수 있을까요? 

답은 기저 벡터에 있습니다.  기저 벡터가 어디로 이동하는지만 알면

이 두 벡터들의 선형 결합으로 만들어지는 공간상의 모든 벡터들이 어디로 이동하는지도 알 수 있게 됩니다. 

 

예를 들어, 벡터 v(-1, 2)는 -1 * i-hat(1,0) + 2 * j-hat(0,1)으로 표현할 수 있습니다. 

선형 변환 이후에도 이 관계는 유지됩니다. ( 벡터 v를 만들기 위한 기저 벡터들의 조합은 일정)

만약에 i-hat(1,0)이 (1,-2)로 j-hat(0,1)이 (3,0)으로 선형 변환된다면

벡터 v(-1, 2)는 기존의 선형 결합 조합을 바뀐 기저 벡터에 대해 수행하므로 

-1 * (1, -2) + 2 * (3, 0) = (5, 2) 가 됩니다. 

 

이는 어떤 벡터 (x, y)든 선형 변환 후에는 (x × (변환된 i-hat) + y × (변환된 j-hat))이 된다는 것을 보여줍니다.

행렬과 선형 변환의 관계

선형 변환은 행렬의 형태로 표현됩니다. 

이때 행렬의 각 열은 각각의 기저 벡터가 변환될 위치를 나타냅니다. 

예를 들어 다음과 같은 행렬이 주어졌을 때

[ a  b ]
[ c  d ]

첫 번째 열 \begin{bmatrix} a \\ c \end{bmatrix} 는 i-hat(1, 0)이 변환될 위치

두 번째 열 \begin{bmatrix} b \\ d \end{bmatrix} 는 j-hat(0,1)이 변환될  위치

[ a  b ] × [ x ] = [ ax + by ]
[ c  d ]   [ y ] = [ cx + dy ]

이 행렬에 벡터 [x, y]를 곱하면, 그 벡터가 선형 변환 이후 어디로 이동하는지를 알 수 있습니다.

 

다시 정리해보면 기저 벡터들의 선형 결합을 통해 공간상의 모든 벡터를 표현하기 때문에 

선형 변환 이후에도 변환된 기저 벡터들을 가지고 이전과 동일한 선형 결합을 하면 벡터가 어디로 이동했는지를 알 수 있습니다. 

 

다음 그림들을 통해서도 확인할 수 있듯이 선형 변환(기저 벡터에 행렬이 곱해졌을 때) 해당 공간을 나타내는 좌표 격자가 변화합니다.

결국은 좌표 격자 상에 있던 모든 점들(벡터)들도 이에 따라 함께 이동합니다. 

 

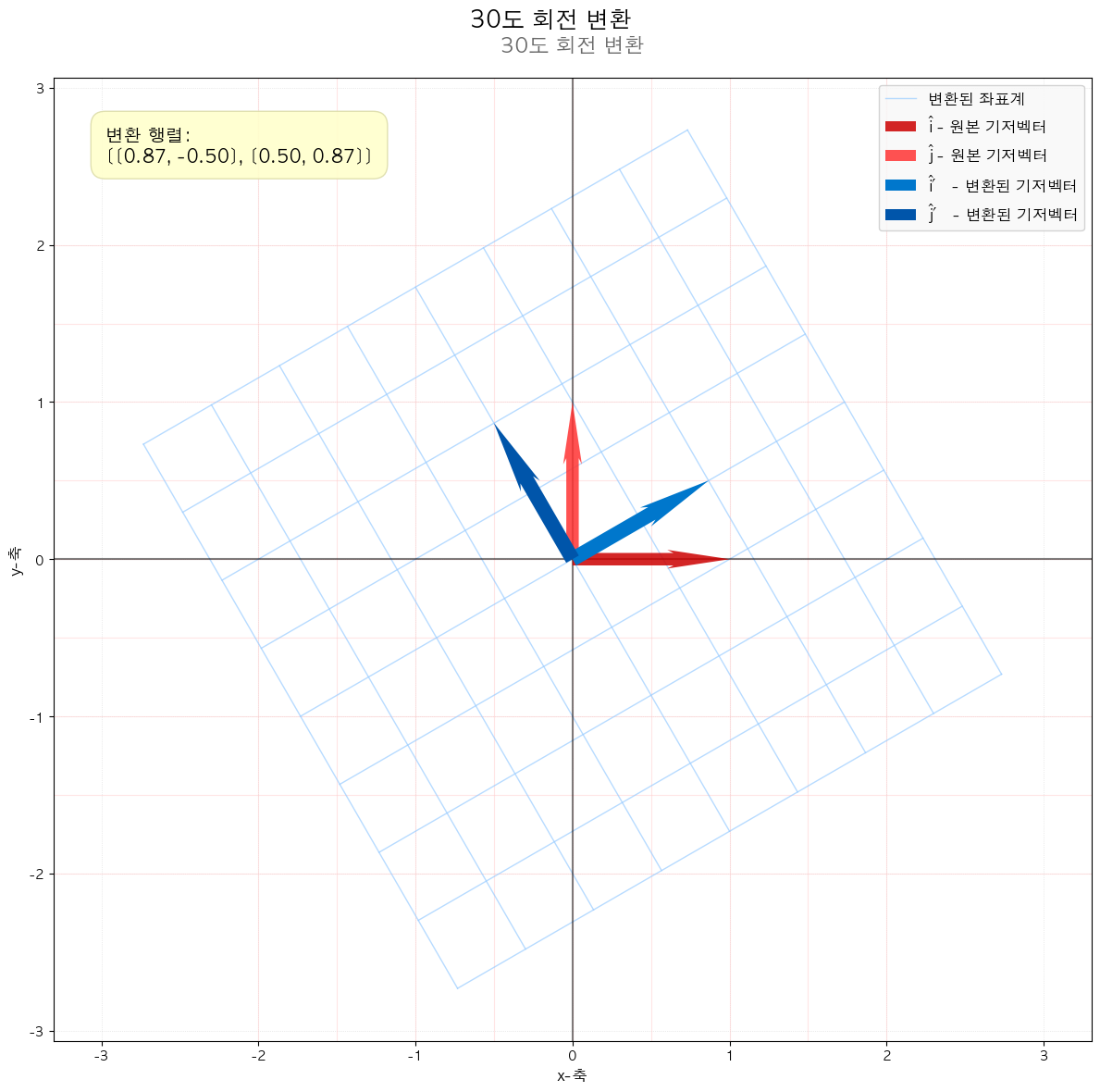
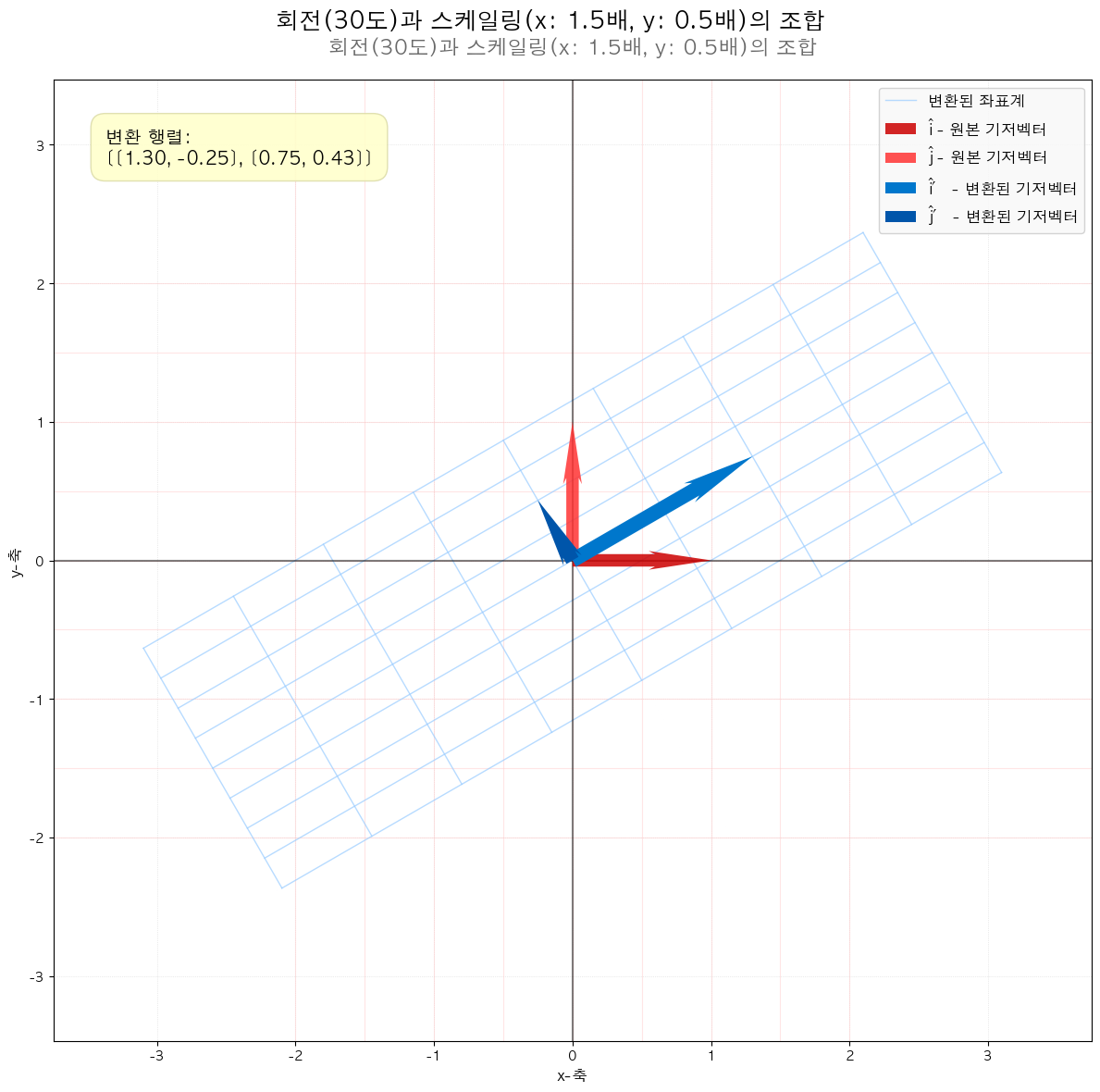
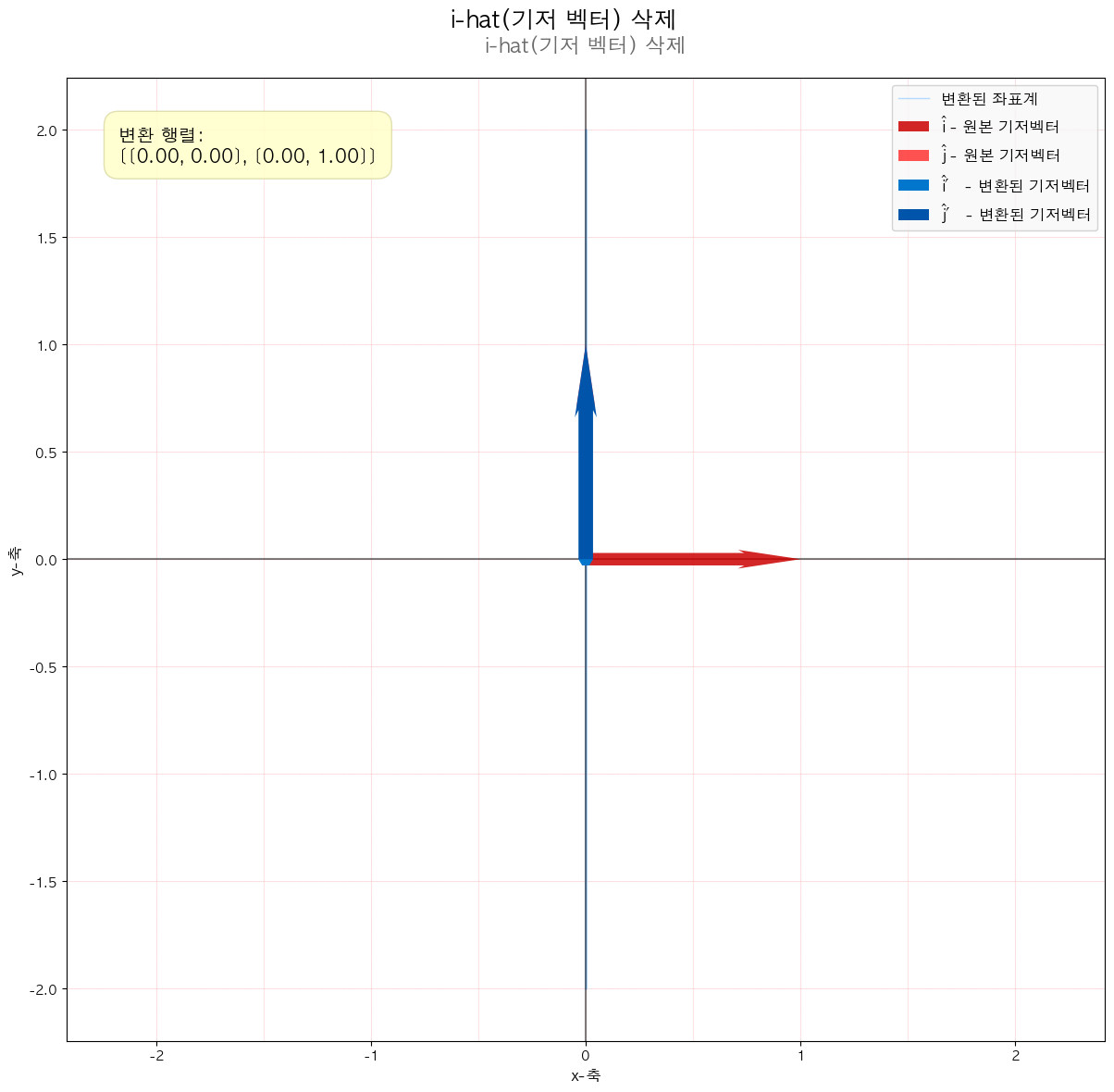
애니메이션을 통해 변화과정을 좀 더 확실히 해볼 수 있습니다. 

 

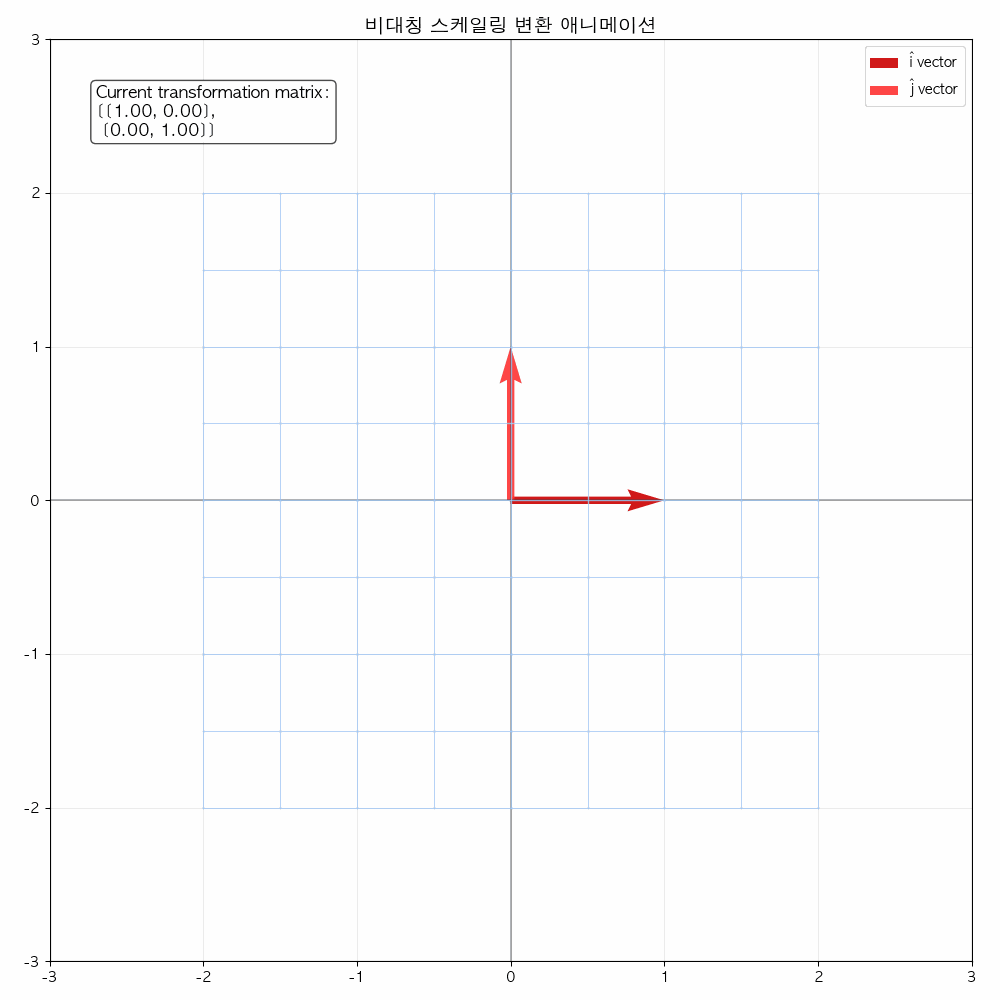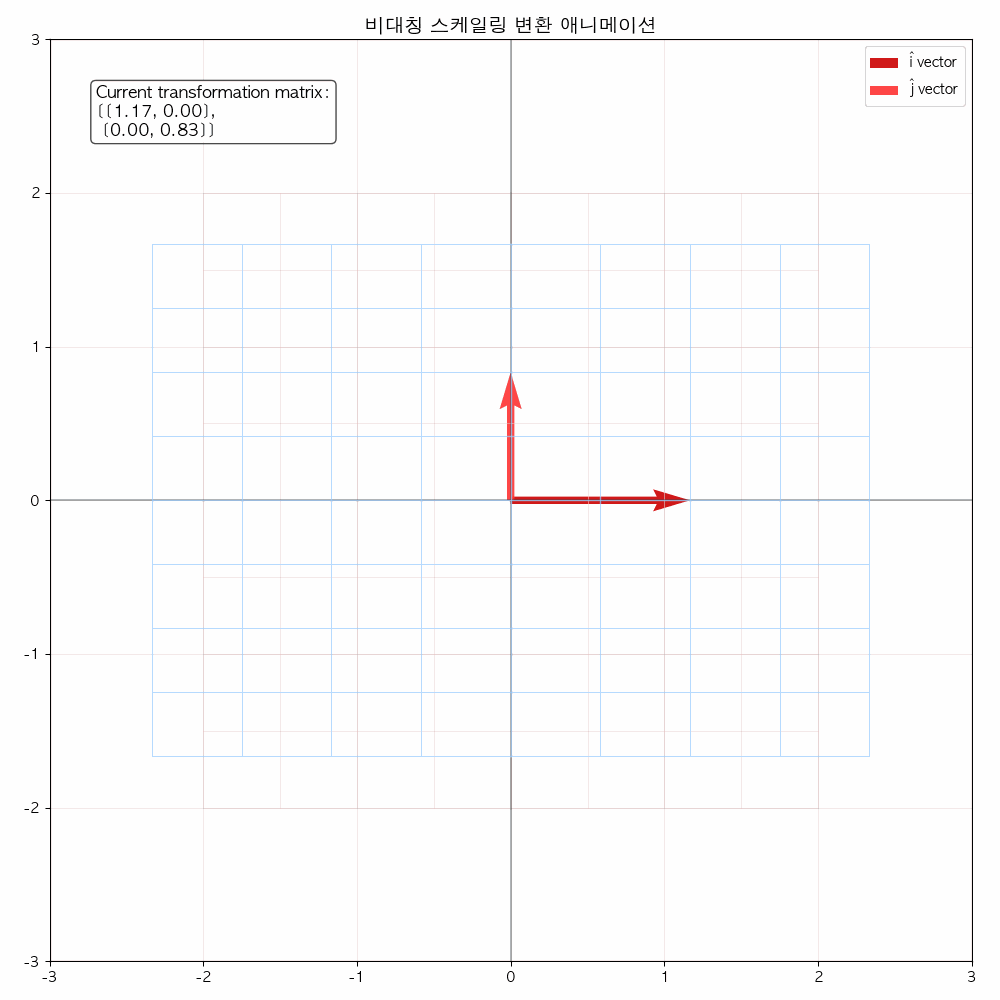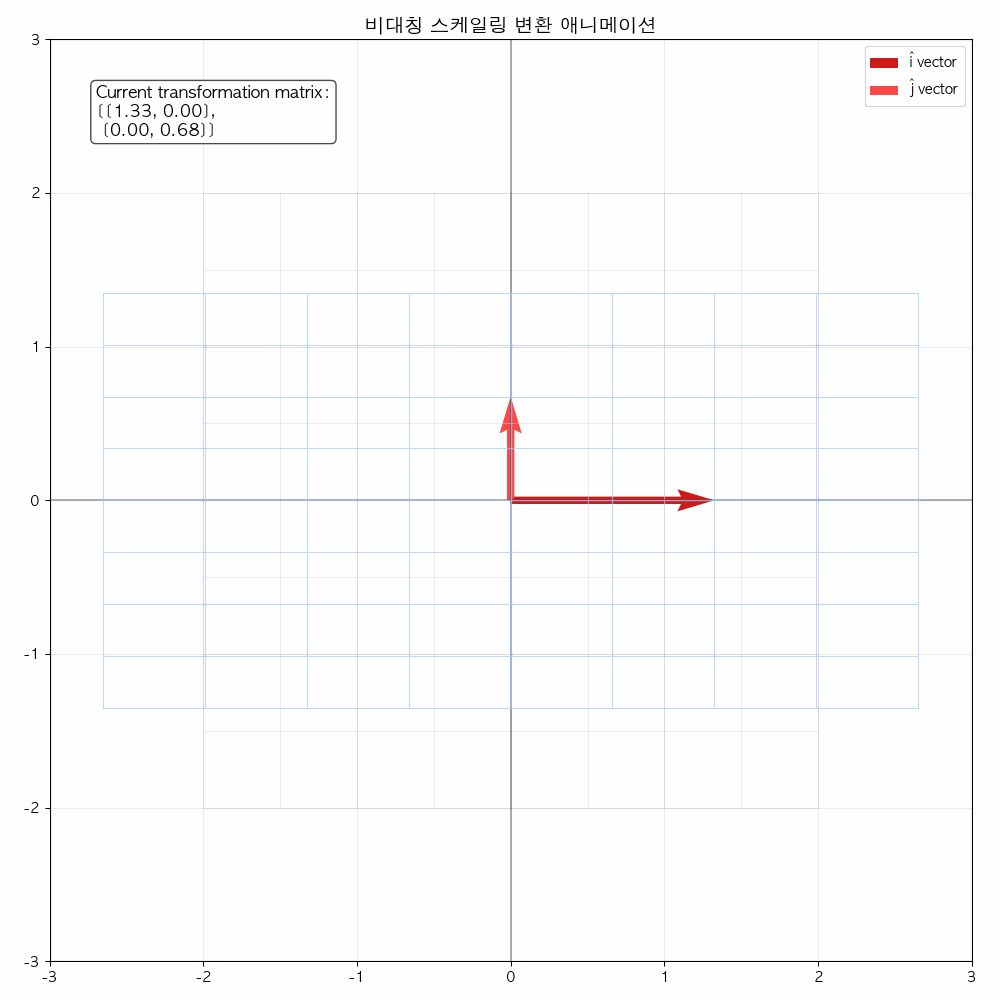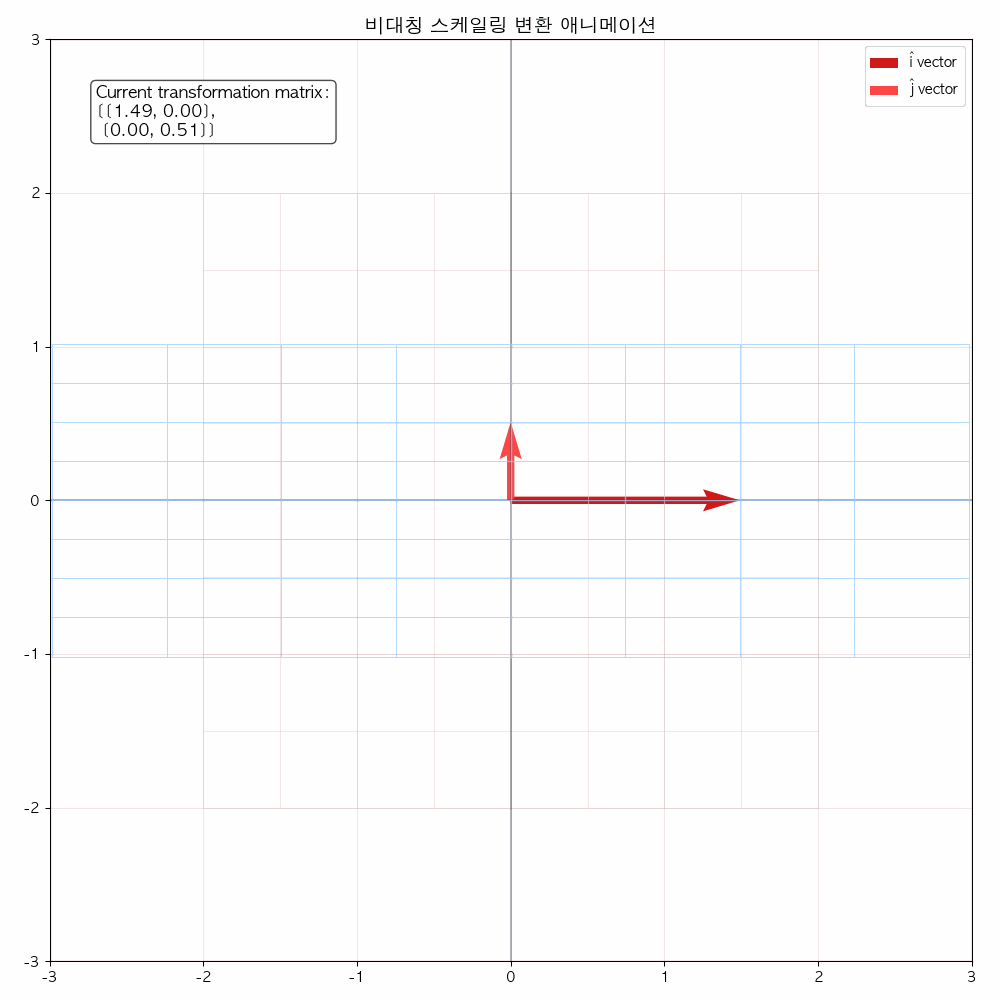
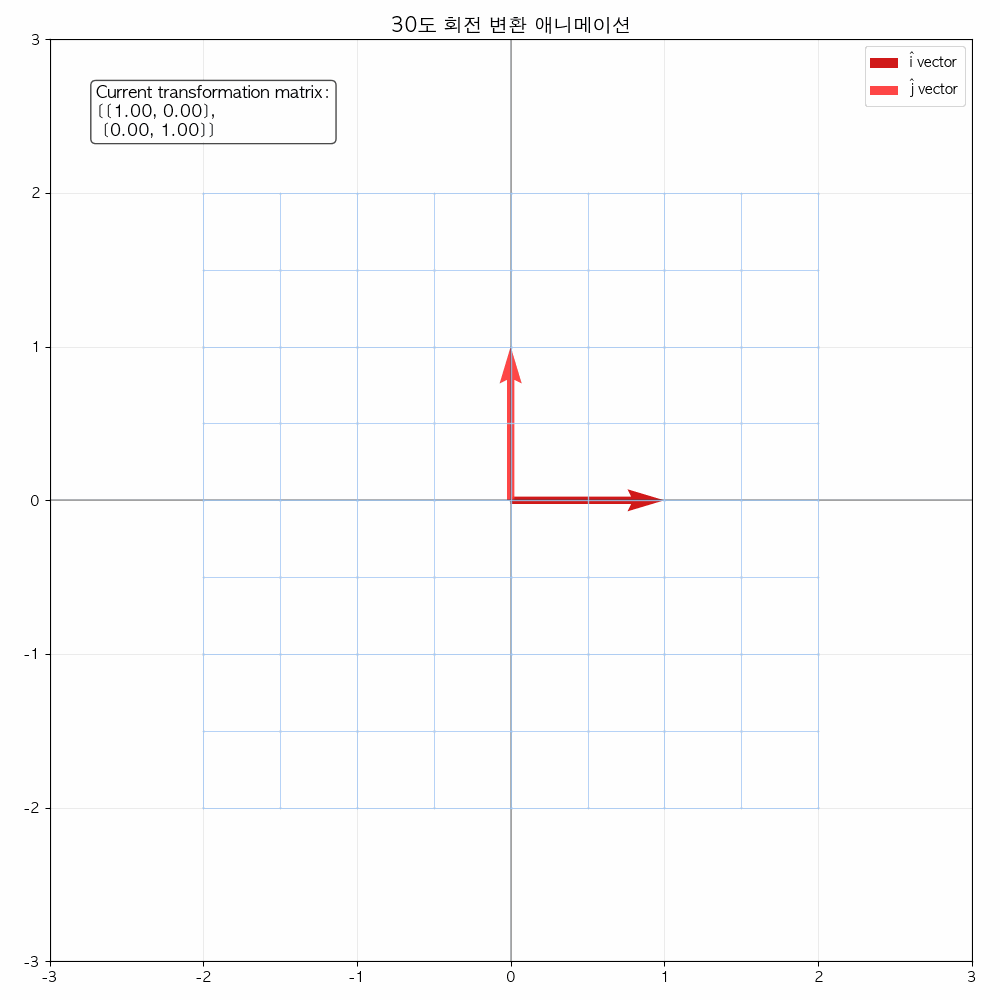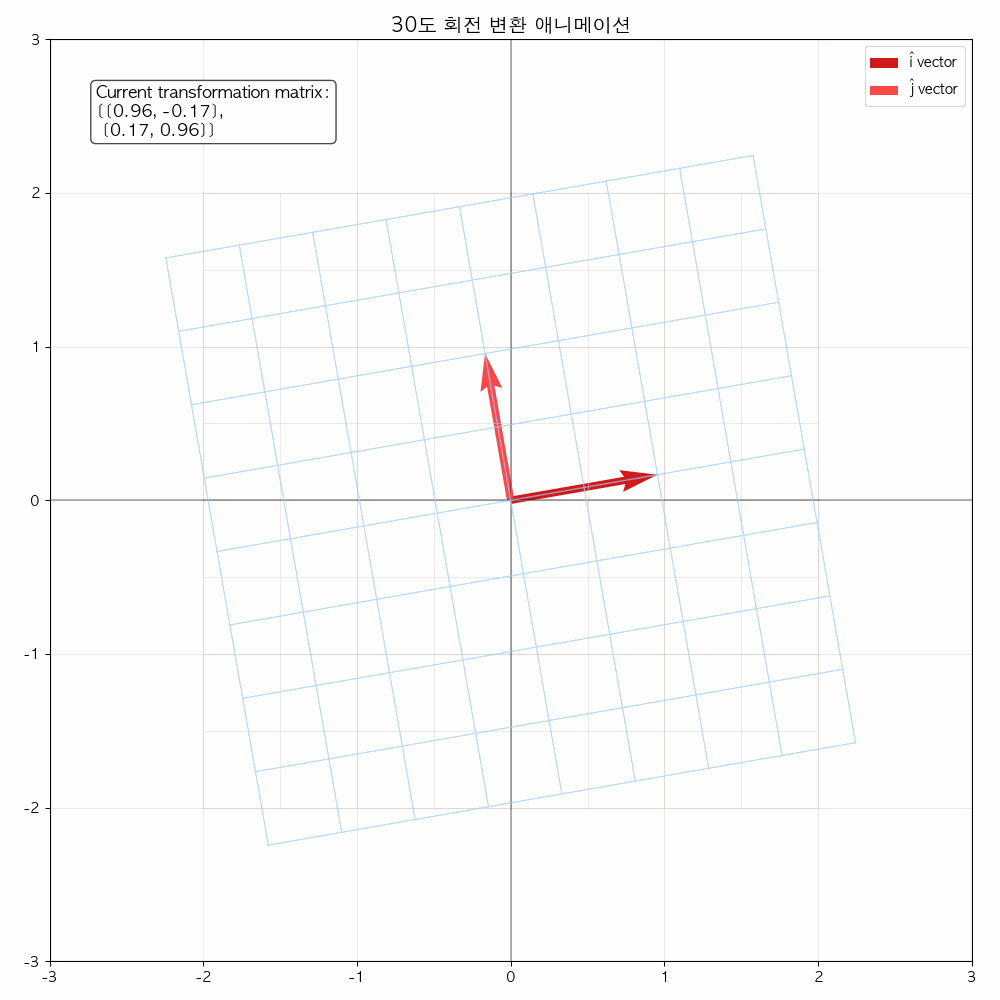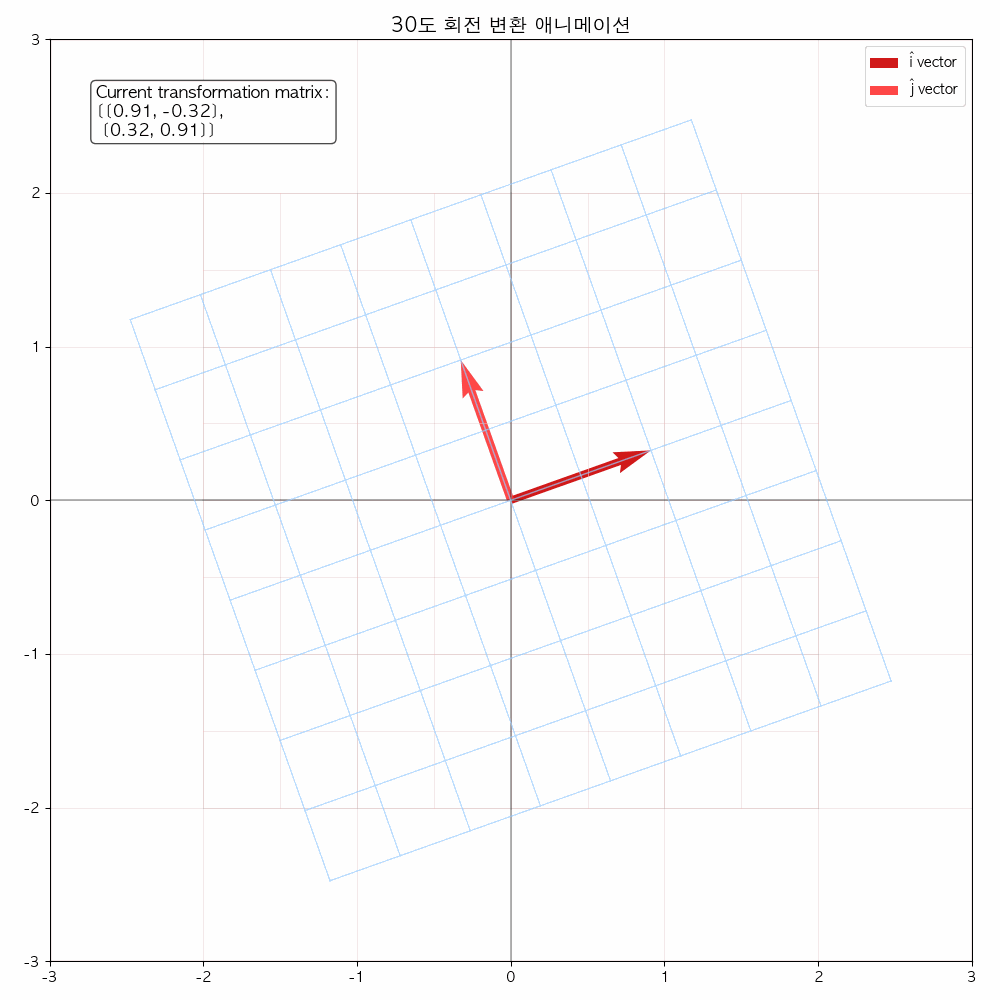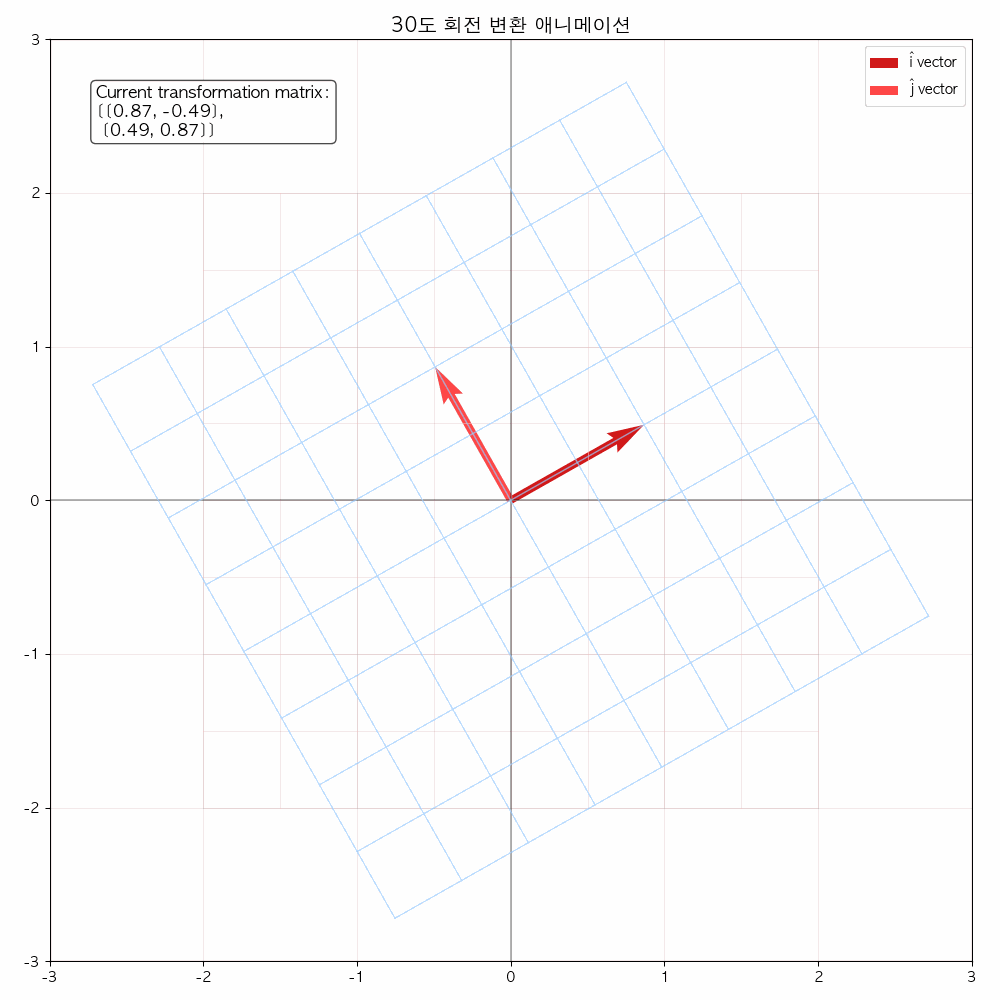
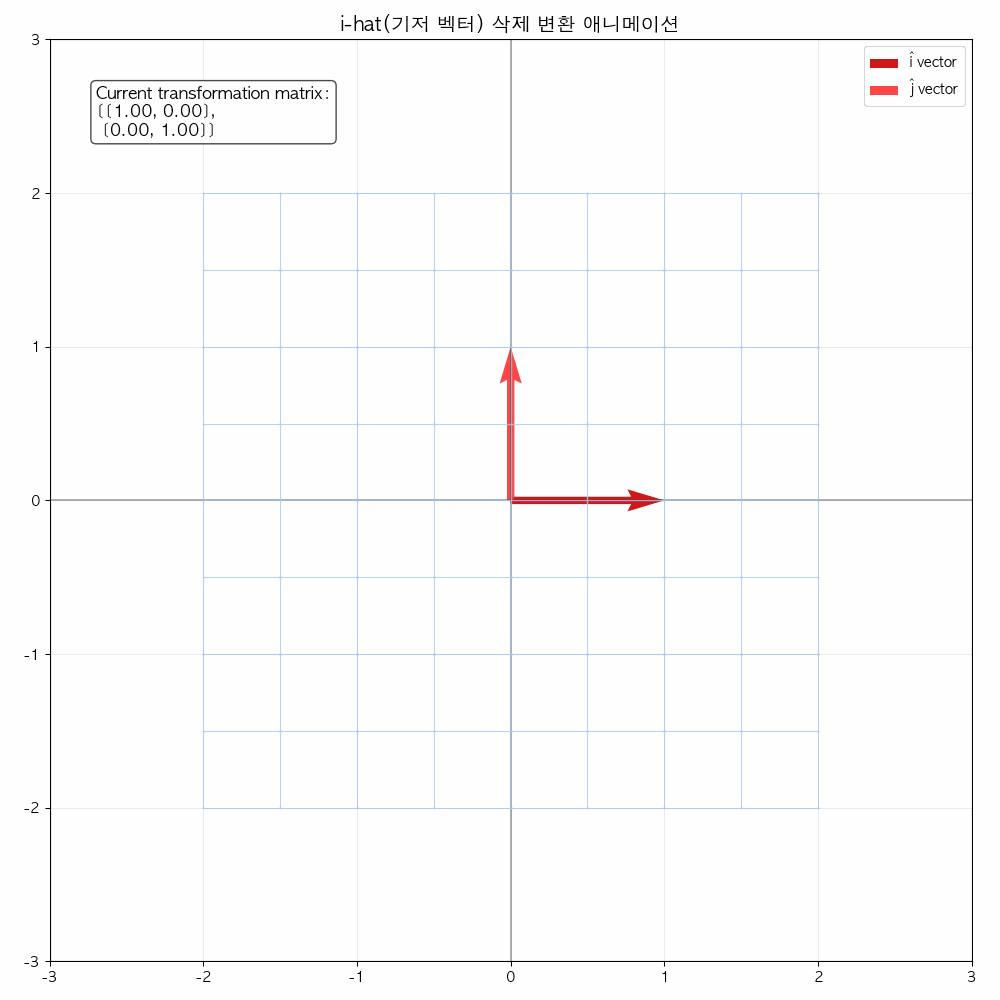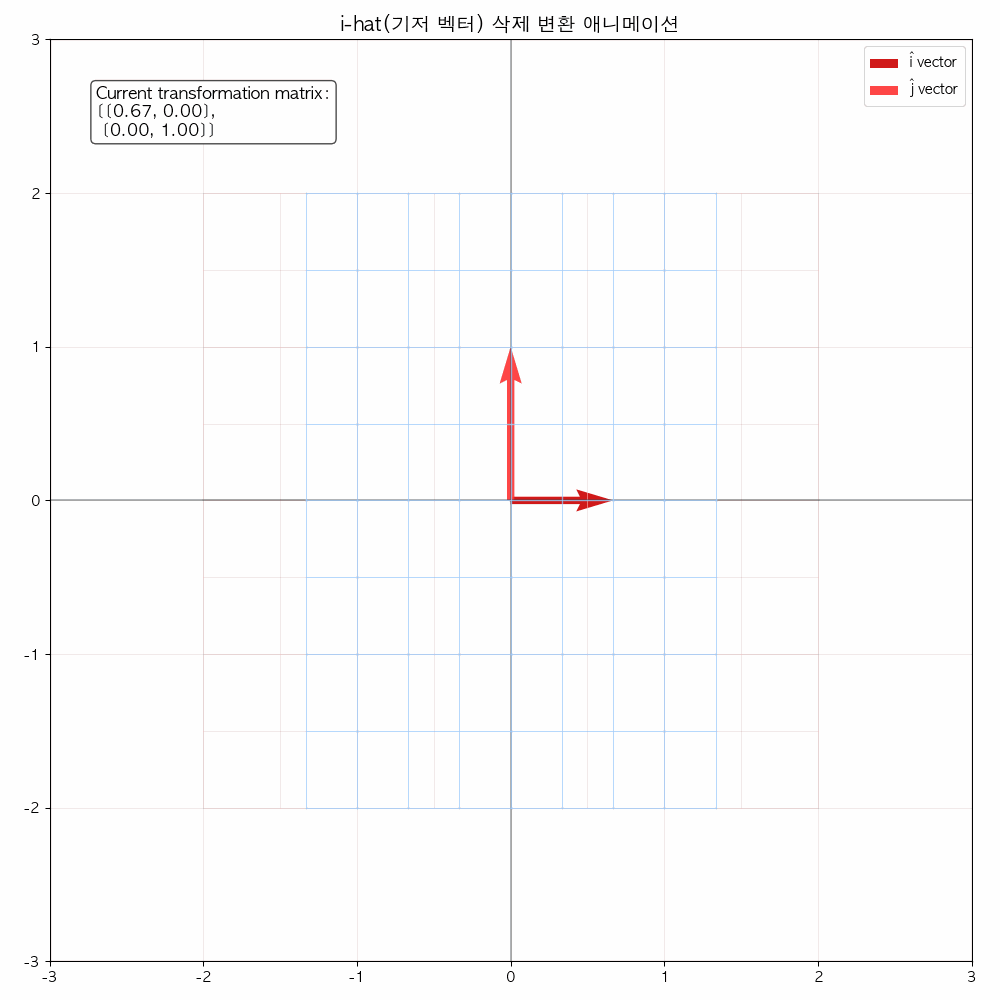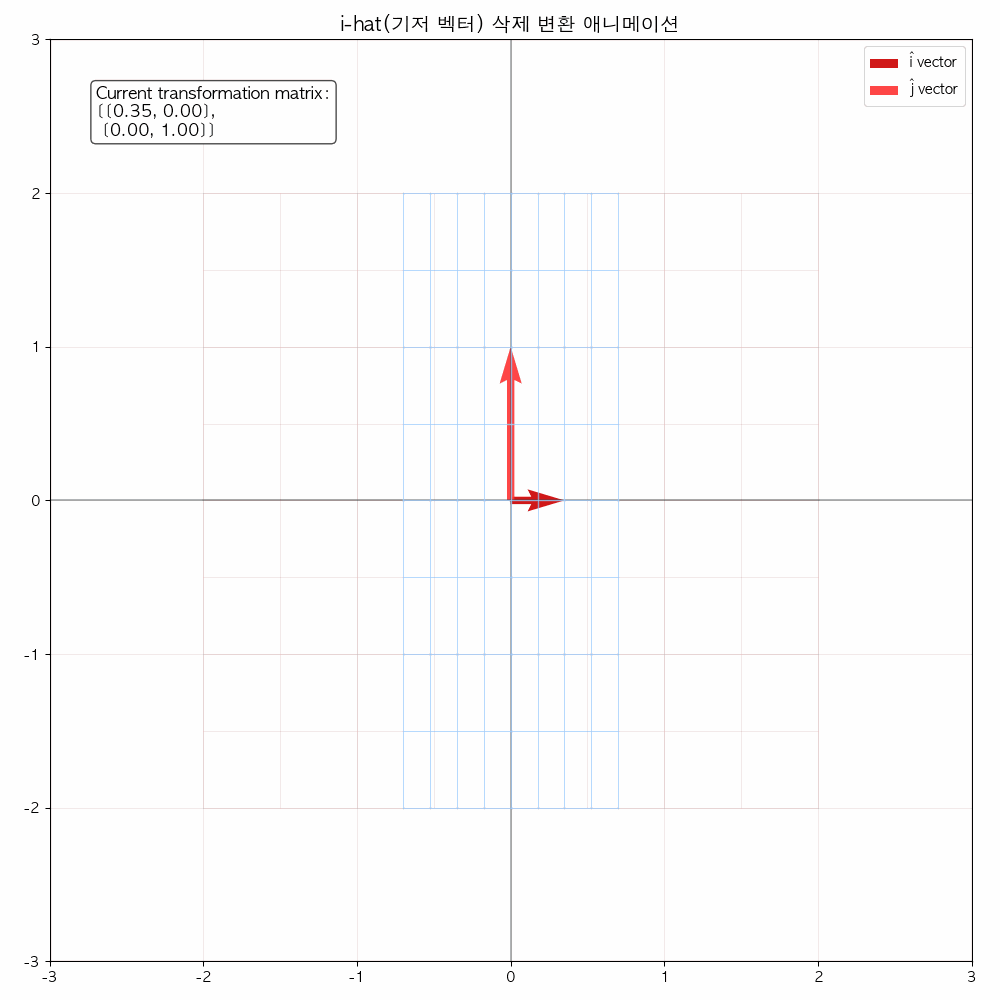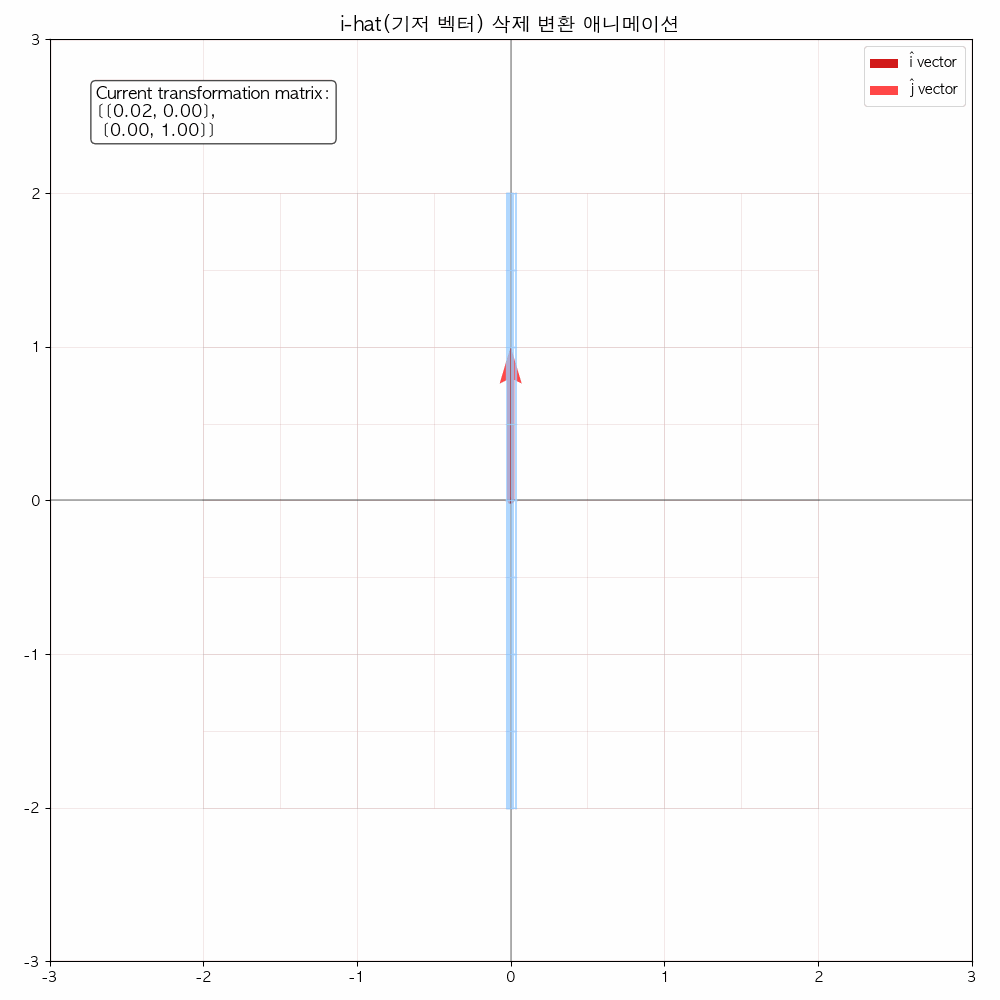
참고 영상 

코드 

GitHub - OneMoreThink/Linear_Algebra