Span : 영역 전개 (領域展開)

Span : 기저 벡터들의 선형 결합으로 영역(공간) 전개하기

 

벡터 좌표를 스칼라로 이해하기

벡터를 숫자 쌍(또는 더 많은 차원에서는 숫자 집합)으로 표현하는 것에 익숙할 것입니다. 예를 들어, 2차원 벡터 (3, -2)는 x축으로 3단위, y축으로 -2단위 이동한 위치를 가리킵니다. 하지만 이 좌표들을 단순히 위치 정보로만 생각하는 것이 아니라, 스칼라(scalar)로 생각해보는 새로운 관점이 있습니다.

스칼라란 무엇일까요? 스칼라는 벡터를 늘리거나 줄이는 역할을 하는 단순한 숫자입니다. 이러한 관점에서, 벡터 좌표는 특별한 벡터들을 스칼라 배수만큼 늘리거나 줄인 다음 더한 결과로 볼 수 있습니다.

2차원 좌표계에서는 두 개의 특별한 벡터가 있습니다.

• i-hat(î): x축 방향으로 길이가 1인 단위벡터
• j-hat(ĵ): y축 방향으로 길이가 1인 단위벡터

이제 벡터 (3, -2)를 다시 생각해보면

• x좌표 3은 i-hat을 3배 늘린 벡터 3î를 의미합니다.
• y좌표 -2는 j-hat을 -2배(방향을 뒤집고 2배 늘림) 한 벡터 -2ĵ를 의미합니다.

최종 벡터는 이 두 벡터의 합, 즉 3î + (-2ĵ)이 됩니다. 이것이 바로 선형대수학에서 매우 중요한 개념인 두 개의 스케일된 벡터의 합입니다.

기저벡터: 좌표계의 기초

위에서 언급한 i-hat과 j-hat은 특별한 이름이 있습니다. 이들은 함께 좌표계의 기저(basis)를 형성합니다. 기저란 무엇일까요?

좌표를 스칼라로 생각할 때, 기저벡터는 이 스칼라들이 실제로 확대/축소하는 대상입니다.

흥미로운 점은, 우리가 다른 기저벡터를 선택하여 완전히 새로운 좌표계를 만들 수 있다는 것입니다. 예를 들어, 오른쪽 위를 가리키는 벡터와 오른쪽 아래를 가리키는 벡터를 새로운 기저벡터로 선택할 수 있습니다. 그리고 새로운 기저 벡터로 구성된 새로운 좌표계에서는 같은 벡터도 다른 '스칼라'로 표현됩니다. 

앞서 i-hat (1,0) 와 j-hat (0,1)을 기저 벡터로 만든 좌표계에서 표현한 벡터 (3, -2) 새로운 기저 벡터 $v_1, v_2$에서는 (0.33, 2.33)으로 표현됩니다. 

선형결합: 벡터 공간의 기본 구성 요소

두 벡터를 스칼라로 곱한 다음 더하는 과정을 해당 벡터의 선형결합(linear combination)이라고 합니다. 
$$a\vec{v} + b\vec{w}$$
쉽게 말해 각 벡터들에 대해 스칼라를 이용해 늘였다, 줄였다한 벡터들의 조합으로 새로운 벡터를 결합해내는 과정을 말합니다.

 

"선형"이라는 단어는 어디서 왔을까요? 왜 이것이 직선과 관련이 있을까요?

두 개의 스칼라 중 하나를 고정하고 다른 하나를 자유롭게 변화시키면, 결과 벡터의 끝점이 직선을 그립니다. 이것이 "선형"이라는 이름의 직관적인 이유입니다. 즉 스칼라 변화가 벡터들의 조합 결과에 대해 선형적으로 반영되기 때문입니다. 

벡터의 생성(span): 도달 가능한 공간 탐색

두 벡터의 가능한 모든 선형결합으로 만들 수 있는 벡터들의 집합을 해당 벡터들의 생성(span)이라고 합니다. 2차원 공간에서 두 벡터의 생성은 다음 두 가지 경우로 나뉩니다.

1. 일반적인 경우: 두 벡터가 서로 다른 방향을 가리키면, 그들의 생성은 모든 2차원 벡터를 포함합니다.
2. 특수한 경우: 두 벡터가 같은 방향을 가리키면, 그들의 생성은 원점을 지나는 하나의 직선상에 있는 벡터들로 제한됩니다.
3. 극단적인 경우: 두 벡터가 모두 영벡터라면, 생성은 원점 하나뿐입니다.

벡터들의 집합을 시각화할 때는 종종 각 벡터를 하나의 점으로 표현합니다. 이렇게 하면 직선 위에 있는 모든 벡터는 그냥 직선 자체로, 2차원 평면의 모든 벡터는 2차원 평면 자체로 시각화할 수 있습니다. 즉, 개별 벡터를 생각할 때는 화살표로, 벡터들의 집합을 생각할 때는 점들로 시각화하는 것이 편리합니다. ( 현재 위의 그림에서 초록색으로 표현된 부분들이 벡터들을 점으로 표현한 것입니다. )

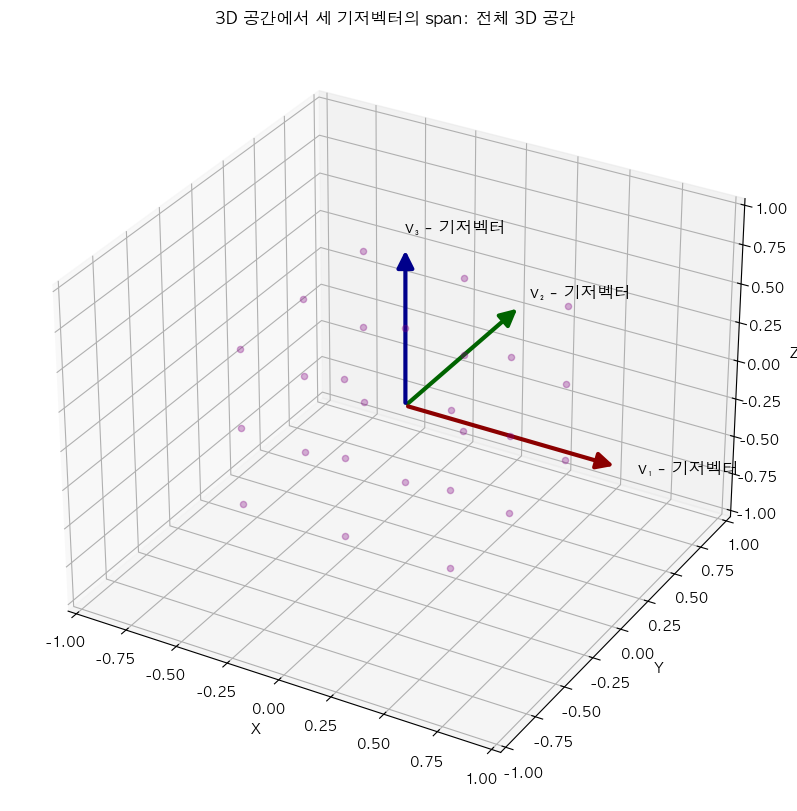
3차원에서의 생성: 평면에서 공간으로

3차원 공간에서 생성은 어떨까요? 서로 다른 방향을 가리키는 두 3차원 벡터의 생성은 어떤 모양일까요? 그것은 원점을 지나는 평면(2차원 평면)이 됩니다! 이 평면은 두 벡터를 다양한 스칼라로 곱하고 더해서 얻을 수 있는 모든 가능한 벡터를 포함합니다.

 

이제 세 번째 벡터를 추가하고 세 벡터의 생성을 고려해봅시다. 두 가지 가능성이 있습니다.

1. 세 번째 벡터가 이미 처음 두 벡터의 생성 내에 있는 경우, 생성은 변하지 않고 원래의 평면으로 유지됩니다.
2. 세 번째 벡터가 그 평면 밖에 있는 경우, 생성은 전체 3차원 공간으로 확장됩니다!

이것은 마치 처음 두 벡터가 만드는 평면이 세 번째 벡터에 의해 전체 공간으로 "팽창" 것처럼 생각할 수 있습니다.

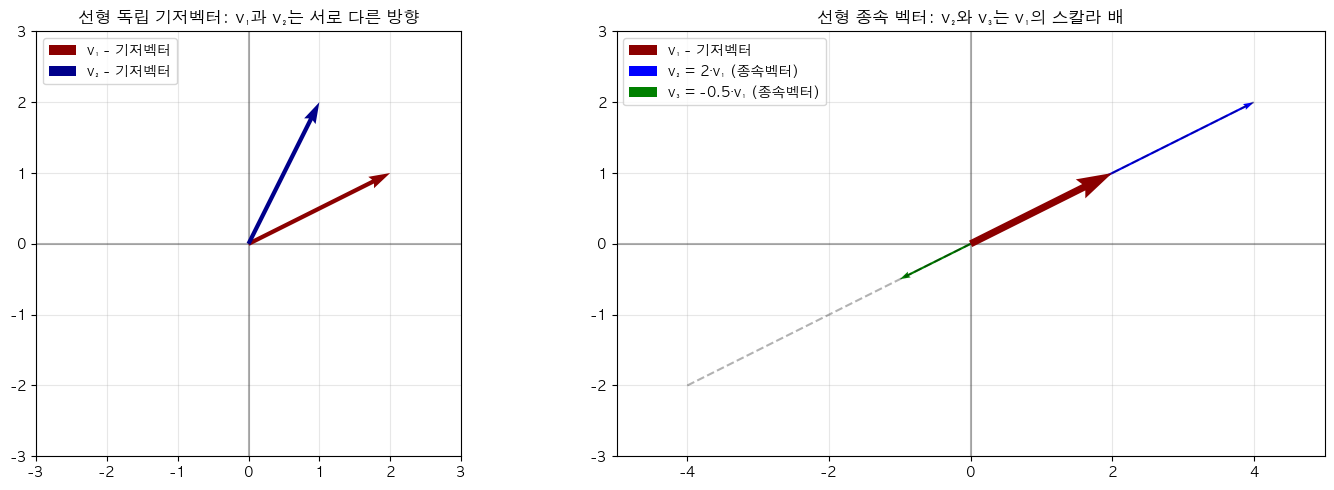
선형 독립과 종속

벡터 집합이 선형 종속(linearly dependent)이라는 것은 집합의 적어도 하나의 벡터가 다른 벡터들의 선형결합으로 표현될 수 있다는 의미입니다. 다시 말해, 적어도 하나의 벡터가 "중복"되어 있어서 span에 새로운 차원을 추가하지 않습니다.

반대로, 벡터 집합이 선형 독립(linearly independent)이라는 것은 집합의 어떤 벡터도 다른 벡터들의 선형결합으로 표현될 수 없다는 의미입니다. 각 벡터는 span에 새로운 차원을 추가합니다.

기저의 기술적 정의

공간의 기저는 그 공간을 생성하는 선형 독립 벡터들의 집합입니다.

1. 벡터들이 전체 공간을 span한다. ( 도달성 )
2. 벡터들이 선형 독립이다. ( 최소성 )

첫 번째 조건은 기저 벡터들이 전체 공간을 생성해야 한다는 것을 의미합니다.  그리고 두 번째 조건은 기저가 최소한의 벡터로 구성되어야 한다는 것을 의미합니다 - 만약 벡터 하나를 제거할 수 있다면, 그것은 진정한 기저가 아닙니다. 쉽게 말해, 기저는 "공간을 효율적으로 생성하는 최소한의 벡터 집합"입니다.

 

n차원 공간의 기저는 항상 정확히 n개의 벡터로 구성됩니다.

• 2차원 평면의 기저: 2개의 선형 독립 벡터
• 3차원 공간의 기저: 3개의 선형 독립 벡터

표준 기저는 각 차원에 하나씩 단위 벡터를 포함합니다:

• 2차원: {(1,0), (0,1)}
• 3차원: {(1,0,0), (0,1,0), (0,0,1)}

 

참고 영상 

 

코드 

GitHub - OneMoreThink/Linear_Algebra