2차원 선형 변환 시각화

선형 변환이란 선형 시스템에 임의의 벡터 또는 벡터들의 묶음으로서의 행렬이 입력으로 주어졌을 때의 출력을 얻는 과정이다. 

 

어떠한 선형 시스템이 다음과 같이 주어졌다고 하자. 

 

$$A=\begin{pmatrix}2&-1\\ 1&1\end{pmatrix}$$

 

이 시스템에 임의의 벡터 $\begin{pmatrix}x\\y \end{pmatrix}$가 입력으로 들어가면 시스템에 의한 선형변환된

결과가 시스템의 열벡터의 결합으로 나타나게 된다. 

 

$$\begin{pmatrix}u\\v\end{pmatrix}=\begin{pmatrix}2&-1 \\ 1&1 \end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=x\begin{pmatrix}2\\1\end{pmatrix}+y\begin{pmatrix}-1\\1\end{pmatrix}$$

 

위와 같은 선형변환 과정을 시각화를 통해 직관적으로 이해해 보도록 하자   

 

시각화 전략

 

1. 선형변환 과정을 좀더 단순화하여 볼 수 있도록  $x-y$ 평면에 직사각형 형태로 배열된 점들을 만들어 입력으로 준다. 

2. 변환과정을 인지하기 쉽도록 점들을 일정한 범위로 그룹화하여 개별의 색을 주었다. 

3.  선형변환으로 인한 변화과정을 보기 위해서 각 과정을 단계별로 나누었다. 

4. 각 단계별 과정을 plot하고 각각을 이미지 파일로 저장하였다. 

5. 각각의 이미지 파일을 gif 파일로 바꾸었다.

 

파이썬을 이용한 시각화에 앞서 먼저 필요한 라이브러리를 import 한다. 

## 필요한 라이브러리 import
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

 

 

먼저 시스템 $A$에 입력으로 넣을 직사각형 형태의 배열된 점을 그려보자 

 

# x-y 평면상에 입력이 될 직사각형 형태 만들기

## 직사각형 공간 나타내는 범위  (min,max,num)
xvals = np.linspace(-4, 4, 9) # -4부터 4(포함)까지 균일한 간격으로 9개의 값을 갖는 배열 생성 
yvals = np.linspace(-3, 3, 7) # -3부터 3(포함)까지 균일한 간격으로 7개의 값을 갖는 배열 생성

## 이중 반복문으로 2D 좌표축상에 표현될 점들 목록을 xvals와 yvals를 조합으로 만들기 
## np.column_stack은 1차원 배열을 2차원 배열로 만들어서 x-y 좌표상에 표현될 점 만들기 
xygrid = np.column_stack([[x, y] for x in xvals for y in yvals])

 x축 값의 범위는  -4에서 4까지이고 y축 값의 범위는 -3에서 3까지이고,

설정한 범위의 점들의을 x-y 쌍으로 하여  열 방향으로 쌓음으로직사각형 형태의 그리드를 만들었다. 

 

xygrid 결과로 x값과 y값의 모든 조합으로 가능한 열벡터들이 나온것을 볼 수 있다. 

x값 하나당 7개의 y값으로 총 x값이 9개 이므로 2 행 (9X7)열 행렬

해당 행렬은 2행으로 구성되어 있음에 따라 리스트로는 [ [1행] [ 2행] ] 형태로 나타난다.

2개의 속성값(x,y좌표)을 갖는 63개의 열벡터들을 만든것이다.

여기서 각 열벡터들이 나타내는 값은 좌표상의 점의 위치이다. 따라서 총 63개의 점이 찍히게 된다.

[[-4. -4. -4. -4. -4. -4. -4. -3. -3. -3. -3. -3. -3. -3. -2. -2. -2. -2.
  -2. -2. -2. -1. -1. -1. -1. -1. -1. -1.  0.  0.  0.  0.  0.  0.  0.  1.
   1.  1.  1.  1.  1.  1.  2.  2.  2.  2.  2.  2.  2.  3.  3.  3.  3.  3.
   3.  3.  4.  4.  4.  4.  4.  4.  4.]
 [-3. -2. -1.  0.  1.  2.  3. -3. -2. -1.  0.  1.  2.  3. -3. -2. -1.  0.
   1.  2.  3. -3. -2. -1.  0.  1.  2.  3. -3. -2. -1.  0.  1.  2.  3. -3.
  -2. -1.  0.  1.  2.  3. -3. -2. -1.  0.  1.  2.  3. -3. -2. -1.  0.  1.
   2.  3. -3. -2. -1.  0.  1.  2.  3.]]

 

$$xyGrid = \begin{pmatrix}
 -4&-4&\dots&4&4\\ 
 -3&-2&\dots&3&4 
\end{pmatrix}$$

 

# 시스템 A 정의하기 -> 열벡터 (2,1)과 (-1,1)로 구성되어있는 시스템
a = np.column_stack([[2, 1], [-1, 1]]) 
print(a)
# 시스템 A에 grid를 input으로하여 선형변환 
uvgrid = np.dot(a, xygrid) # 선형변환 함수: np.dot(시스템,인풋)

선형 변환 결과 

[[ -5.  -6.  -7.  -8.  -9. -10. -11.  -3.  -4.  -5.  -6.  -7.  -8.  -9.
   -1.  -2.  -3.  -4.  -5.  -6.  -7.   1.   0.  -1.  -2.  -3.  -4.  -5.
    3.   2.   1.   0.  -1.  -2.  -3.   5.   4.   3.   2.   1.   0.  -1.
    7.   6.   5.   4.   3.   2.   1.   9.   8.   7.   6.   5.   4.   3.
   11.  10.   9.   8.   7.   6.   5.]
 [ -7.  -6.  -5.  -4.  -3.  -2.  -1.  -6.  -5.  -4.  -3.  -2.  -1.   0.
   -5.  -4.  -3.  -2.  -1.   0.   1.  -4.  -3.  -2.  -1.   0.   1.   2.
   -3.  -2.  -1.   0.   1.   2.   3.  -2.  -1.   0.   1.   2.   3.   4.
   -1.   0.   1.   2.   3.   4.   5.   0.   1.   2.   3.   4.   5.   6.
    1.   2.   3.   4.   5.   6.   7.]]

 

 

시스템 $A$를 구성하는 열벡터들을 정의하고 

np.dot(a,grid) 를 통해 시스템 $A$에 위에서 정의한 직사각형 형태의 grid를 입력을 주어 선형변환을 하였다. 

 

$$uvGrid = A\cdot xyGrid$$

 

 

이제 선형변환에 대한 연산은 완료하였으며 선형 변환 과정을 이미지화하기 위한 과정을 살펴보자. 

 

다음 코드는 선형 변환 과정을 좀더 명확하기 위해 각 x-y좌표에 대해 색(RGB)을 매핑하는 함수를 정의하였다. 

R과 G는 y값에 대해서 조정되며, B는 x값에 대해서 조정된다. 

나타나는 이미지는 수평방향에 대해서는 비슷한 색을 유지하지만 수직 방향에 대해서는 구분되는 색을 가지게 된다. 

# 선형 변환의 각 과정을 구분하기 쉽도록 좌표에 따라 색을 지정하는 함수 

def colorizer(x, y):
 
    # min(상한,계산되는 값) -> 계산되는 값이 상한 보다 클경우 상한 반환
    r = min(1, 1-y/3) 
    g = min(1, 1+y/3)
    b = 1/4 + x/16
    return (r, g, b) # x,y 좌표에 따라 매핑된 RGB 값을 튜플로 반환

 

 

위에서 정의한 색을 지정하는 함수를 xygrid의 각 열벡터(점)에 적용해서 점 개수만큼의 RGB색조합을 튜플 리스트로 뽑아낸다음에

polt하는 과정에서 뽑은 색상을 각 점들과 매핑시켜준다. 

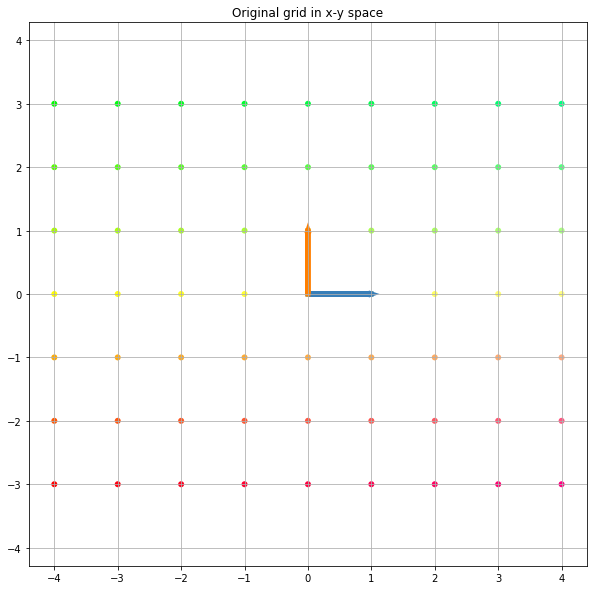
# map함수는 첫번째 인자로 주어진 함수를 두번째, 세번째로 주어진 리스트의 요소들에 적용한다. 
# 예를 들어 2행으로된 xygrid의 첫번째 요소[0]은 x좌표값들이 들어있고
# xygrid의 두번째 요소[1]은 y좌표값들이 들어있다. 
# 각 리스트의 요소들을 하나씩 가져와서 위에서 정의한 colorizer 함수에 인자로 넣는다. 
# 그러면 xygrid의 열 개수만큼 RGB 색상을 나타내는 튜플들로 구성된 리스트를 얻는다. 
colors = list(map(colorizer, xygrid[0], xygrid[1]))

# 점들을 좌표위에 나타낸다. 
plt.figure(figsize=(4, 4), facecolor="w") # plot 사이즈와 바탕 색 지정
# scatter(x좌표리스트,y좌표리스트,점크기,각 좌표의 색)
plt.scatter(xygrid[0], xygrid[1], s=36, c=colors, edgecolor="none")

# Set axis limits
plt.grid(True)
plt.axis("equal")
plt.title("Original grid in x-y space")

코드의 결과로 다음과 같은 이미지를 얻을 수 있다. 

 

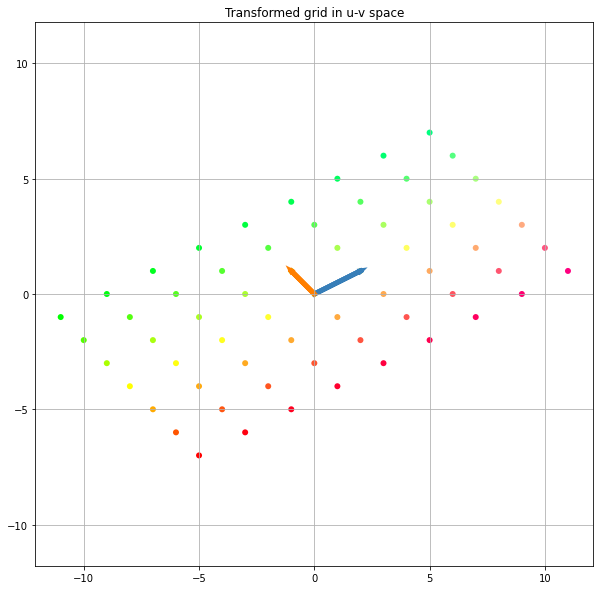
# Plot transformed grid points
plt.figure(figsize=(10,10), facecolor="w")
plt.scatter(uvgrid[0], uvgrid[1], s=36, c=colors, edgecolor="none")
plt.grid(True)
plt.axis("equal")
plt.title("Transformed grid in u-v space")

선형변환된 결과도 입력과 같이 코드를 이용해 나타내면 

 

선형변환되는 과정을 연속적으로 나타내기 위해 중간 변환과정을 나타내는 stepwise_transform 함수를 정의하면

 

# 중간변환과정을 보기위하여 중간 과정에 적용할 행렬을 시스템 A에 대해 보간법을 이용해서 구한뒤 
# 입력이 되는 점집합에 대해 선형변환하여 중간과정이 되는 결과들을 얻는다. 

# a는 시스템 행렬로 2x2/ points는 입력이될 열벡터로 구성된 행렬(점집합) / nsteps = 중간과정 수
def stepwise_transform(a, points, nsteps=30):
    '''
    Generate a series of intermediate transform for the matrix multiplication
      np.dot(a, points) # matrix multiplication
    starting with the identity matrix, where
      a: 2-by-2 matrix
      points: 2-by-n array of coordinates in x-y space 

    Returns a (nsteps + 1)-by-2-by-n array
    '''
    # 주어진 점배열(points)만큼의 원소의 개수를 갖고 있는 리스트를 nsteps+1만큼 가지고 있는 리스트 생성
    # 해당 리스트는 이후 중간 변환을 통해 생성된 결과값을 담기 위해 사용된다. 
    transgrid = np.zeros((nsteps+1,) + np.shape(points))
    # 중간 선형 변환과정을 시행
    for j in range(nsteps+1):
        # 2X2의 단위행렬 + (시스템행렬 A - 단위행렬)*현재스텝수 / 전체스텝수  -> (보간법을 위해 중간시스템 행렬 구하기)
        intermediate = np.eye(2) + j/nsteps*(a - np.eye(2))
        # 구한 중간행렬 입력값에 적용하여 중간 결과 얻은후 위에서 만든 transgird에 결과값들 담고
        transgrid[j] = np.dot(intermediate, points) 
        
    return transgrid # 중간변환결과들 반환 

# Apply to x-y grid
steps = 30
transform = stepwise_transform(a, xygrid, nsteps=steps)

 

이 코드는 시스템인 2X2 행렬 $A$에 대한  2Xn 열벡터(점)으로 표현되는 x-y 공간의 점집합에 선형 변환 과정을 단계별로 나누는 함수로

중간변환에 사용될 시스템 행렬은 원래의 행렬 $A$을 보간법을 이용해서 구한 뒤

해당 행렬을 점집합에 적용하여 각 중간 변환 결과를 가져온다. 

 

 

위의 함수를 적용해서 만든 중간 선형변환 결과 값들을 plot한후 생성된 이미지를 모으는 과정이다. 

# 반환된 중간선형변환 결과값을 color를 적용해 plot한 후 생성된 이미지들을 "png-frames" 디렉토리에 담는다. 

def make_plots(transarray, color, outdir="png-frames", figuresize=(4,4), figuredpi=150):
    '''
    Generate a series of png images showing a linear transformation stepwise
    '''
    nsteps = transarray.shape[0]
    ndigits = len(str(nsteps)) # to determine filename padding
    maxval = np.abs(transarray.max()) # to set axis limits
    # create directory if necessary
    import os
    if not os.path.exists(outdir):
        os.makedirs(outdir)
    # create figure
    plt.ioff()
    fig = plt.figure(figsize=figuresize, facecolor="w")
    for j in range(nsteps): # plot individual frames
        plt.cla()
        plt.scatter(transarray[j,0], transarray[j,1], s=36, c=color, edgecolor="none")
        plt.xlim(1.1*np.array([-maxval, maxval]))
        plt.ylim(1.1*np.array([-maxval, maxval]))
        plt.grid(True)
        plt.draw()
        # save as png
        outfile = os.path.join(outdir, "frame-" + str(j+1).zfill(ndigits) + ".png")
        fig.savefig(outfile, dpi=figuredpi)
    plt.ion()

# Generate figures
make_plots(transform, colors, outdir="tmp")

마지막으로 저장한 이미지들을 gif 파일로 변환한다. 

# Convert to gif (works on linux/os-x, requires image-magick)
from subprocess import call
call("cd  ~/Linear-System/VectorSpace/tmp && convert -delay 10 frame-*.png ../animation.gif", shell=True)
# cd ~/이미지들이 저장된 디렉토리 위치 &&
# Optional: uncomment below clean up png files
#call("rm -f png-frames/*.png", shell=True)

변환된 gif는 아래와 같이 나타난다. 

 

처음과 마지막 장면을 비교해보면 $x-y$ 열공간은 열벡터 $x=\begin{pmatrix}1\\0\end{pmatrix} y=\begin{pmatrix}0\\1\end{pmatrix}$을 기저로하여 구성되어 있었다. 

 

선형변환이 된 이후의 공간인 $u-v$ 열공간은 시스템 행렬 $A$을 구성하는 열벡터인 

$u=\begin{pmatrix}2\\1\end{pmatrix} v=\begin{pmatrix}-1\\1\end{pmatrix}$을 기저로 하여 구성된다. 

 

즉 선형변환을 하게 되면 열공간을 구성하는 열벡터의 형태가 시스템을 구성하는 열벡터로 바뀜에 따라 

기존에 열벡터에 매핑되어 있던 공간상의 점들이 바뀐 열벡터에 따라 공간상에 다시 매핑되게 된다. 

위의 경우를 예로 들면 (1,0)에 매핑되어 있던 점이 (2,1)로 바뀜에 따라 주변의 점들도 같은 방식으로 변화함으로서 

공간의 형태가 달라지게 되는 것이다. 

 

 

시스템을 구성하는 열벡터의 모양에 따라 선형변환의 형태가 달라진다. 

따라서 다양한 형태의 선형변환이 가능하다. 

 

 

회전 행렬

각도 $\theta$ 만큼 회전 

 

$$A=\begin{pmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{pmatrix}$$

## Example 2: Rotation
theta = np.pi/3 # 60 degree clockwise rotation
a = np.column_stack([[np.cos(theta), np.sin(theta)], [-np.sin(theta), np.cos(theta)]])
print(a)
# Generate intermediates
transform = stepwise_transform(a, xygrid, nsteps=steps)
make_plots(transform, colors)


# Convert to gif (works on linux/os-x, requires image-magick)
from subprocess import call
call("cd  ~/Linear-System/VectorSpace/png-frames && convert -delay 10 frame-*.png ../animation2.gif", shell=True)
# Optional: uncomment below clean up png files
#call("rm -f png-frames/*.png", shell=True)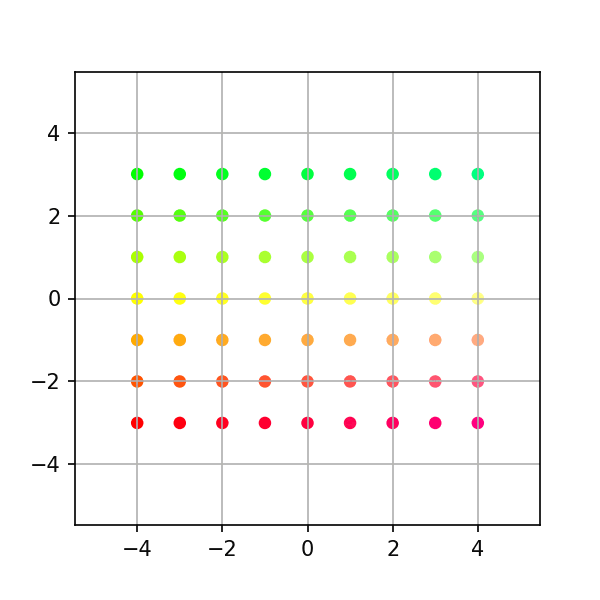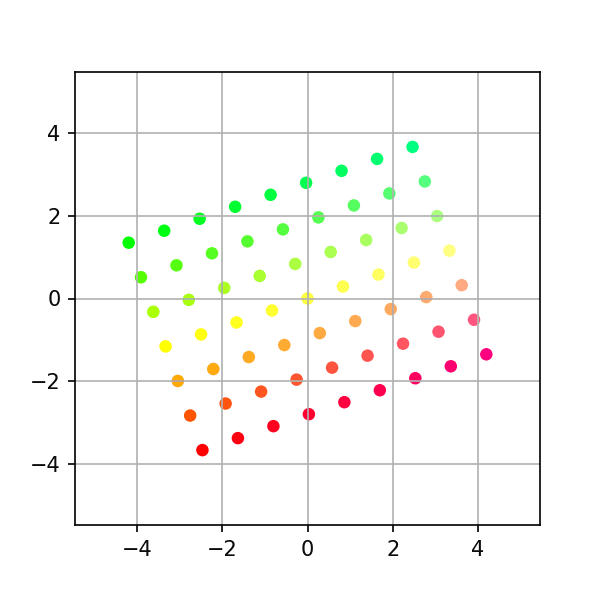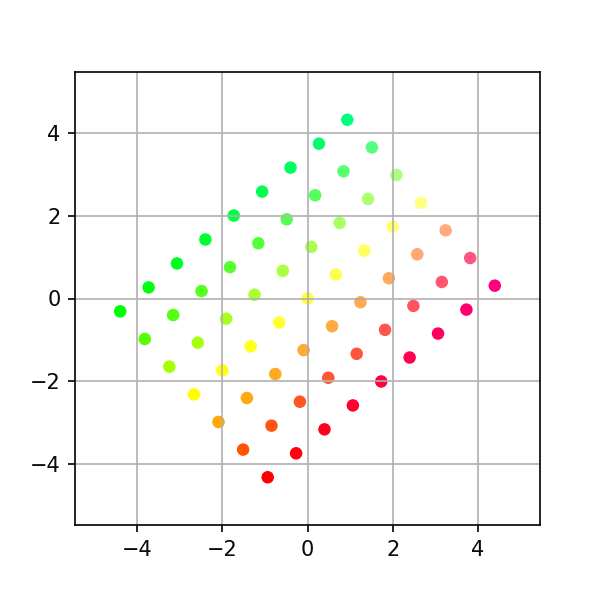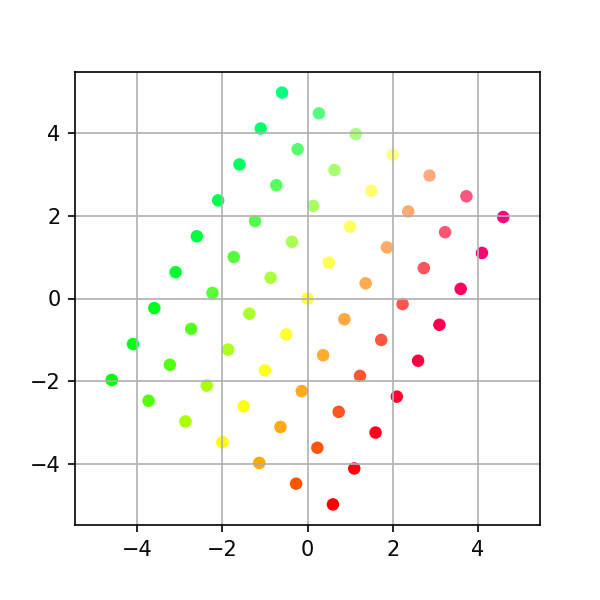

전단행렬

x축방향 전단

 

아래의 경우에는 두번째 열벡터에 없던 x방향 성분이 생기므로 x축방향으로의 전단이 일어난다. 

 

$$A=\begin{pmatrix} 1 & \lambda \\ 0  & 1 \end{pmatrix}$$

# Example 3: Shear
a = np.column_stack([[1, 0], [2, 1]]) # shear along x-axis
print(a)
# Generate intermediates
transform = stepwise_transform(a, xygrid, nsteps=steps)
make_plots(transform, colors)

# Convert to gif (works on linux/os-x, requires image-magick)
from subprocess import call
call("cd  ~/Linear-System/VectorSpace/png-frames && convert -delay 10 frame-*.png ../animation3.gif", shell=True)
# Optional: uncomment below clean up png files
#call("rm -f png-frames/*.png", shell=True)

순열행렬

각 축의 방향을 교환한다.

 

예를 들어 수평방향을 나타내던 x축은 수직 방향을 향하고, 수직 방향을 나타내던 y축은 수평방향을 향한다.

 

$$A=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$$

# Example 4: Permutation
a = np.column_stack([[0, 1], [1, 0]])
print(a)
# Generate intermediates
transform = stepwise_transform(a, xygrid, nsteps=steps)
make_plots(transform, colors)

# Convert to gif (works on linux/os-x, requires image-magick)
from subprocess import call
call("cd  ~/Linear-System/VectorSpace/png-frames && convert -delay 10 frame-*.png ../animation4.gif", shell=True)
# Optional: uncomment below clean up png files
#call("rm -f png-frames/*.png", shell=True)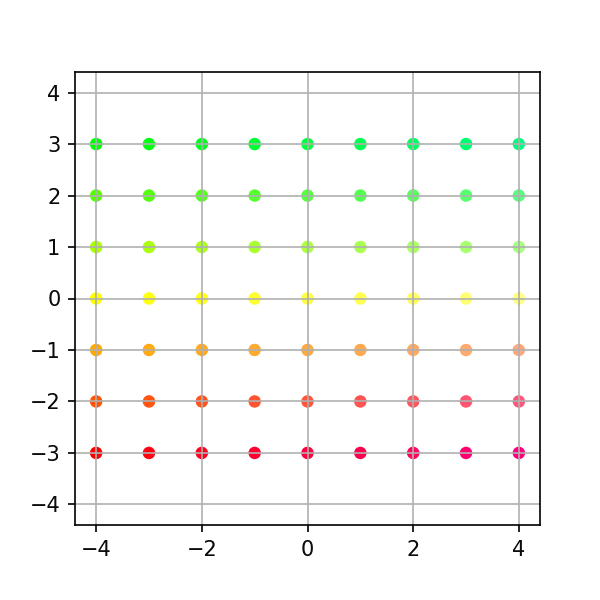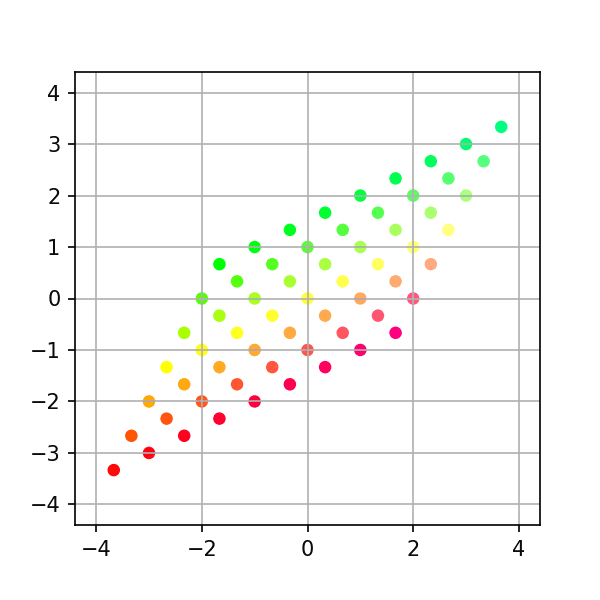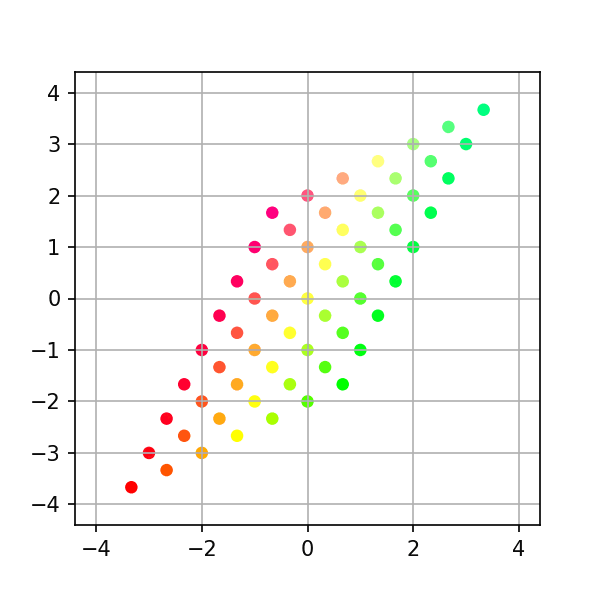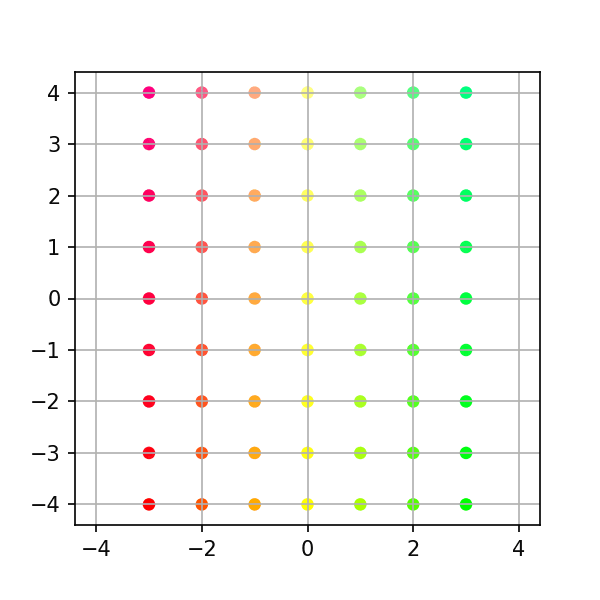

사영

x축방향으로의 정사영

 

두번째 열벡터의 y성분이 없어지면서 y방향을 나타내는 값들이 모두 사라짐에 따라 x축 방향의 값만 남게 된다.

 

$$A=\begin{pmatrix} 1& 0 \\ 0 & 0 \end{pmatrix}$$

# Example 5: Projection
a = np.column_stack([[1, 0], [0, 0]])
print(a)
# Generate intermediates
transform = stepwise_transform(a, xygrid, nsteps=steps)
make_plots(transform, colors)

# Convert to gif (works on linux/os-x, requires image-magick)
from subprocess import call
call("cd  ~/Linear-System/VectorSpace/png-frames && convert -delay 10 frame-*.png ../animation5.gif", shell=True)
# Optional: uncomment below clean up png files
#call("rm -f png-frames/*.png", shell=True)

 

---

★출처★

02. Visualizing 2D linear transformations

 

---