이항 계수 : 뽑을까 말까? / 다항 계수 : 어디에 줄까?

확률은 가능성에 0~1 사이의 숫자를 부여하는 방법으로

가장 기본적인 접근은 '우리가 관심 있는 사건이 일어날 수 있는 경우의 수'를 '가능한 전체 경우의 수'로 나누는 것입니다. 

 

예를 들어, 포커 게임에서 스트레이트 플러시나 풀 하우스와 같은 특정 패가 나올 확률을 계산하려면, 전체 가능한 패 중에서 그런 특정 패가 몇 개나 존재하는지 계산해야 합니다. 하지만 52개나 되는 카드들을 가지고 5개를 뽑았을 때 가능한 조합이 몇 개인지 일일이 세는 것은 쉽지 않습니다. 이렇게 상황이 조금만 복잡해져도 경우의 수를 세는 것이 복잡해지기 때문에 이를 좀 더 쉽게 셀 수 있는 도구가 필요합니다. 

이항 계수 : 순서 구분 없는 샘플링

이항계수는 n개의 객체에서 r개를 선택하는 방법의 수를 계산할 때 사용합니다. 특히 이 경우는

• 순서가 중요하지 않음 (비순서) -> '1' '2' '3' 은 '2' '3' '1'과 동일함 
• 한 번 선택한 객체는 다시 선택할 수 없음 (비복원) -> 뽑은 걸 다시 넣지 않음 

이러한 방식의 선택을 수학적으로 표현하면 "n choose r" 또는 $\binom{n}{r}$로 표기하며, 그 공식은 다음과 같습니다

$$\binom{n}{r} = \frac{n!}{(n-r)! \times r!}$$

 

이항계수를 이용하면 52장의 카드에서 5장을 뽑는 포커 패의 총 경우의 수를 쉽게 계산할 수 있습니다

$$\binom{52}{5} = \frac{52!}{47! \times 5!}$$

이는 52장의 카드에서 5장을 뽑는 가능한 모든 조합의 수를 나타냅니다. 이 값은 약 2,598,960으로, 가능한 모든 포커 패의 수입니다.

파스칼의 삼각형과 이항정리

이항계수는 파스칼의 삼각형을 통해 시각적으로 표현할 수 있습니다. 파스칼의 삼각형은 각 숫자가 바로 위 두 숫자의 합으로 이루어진 삼각형 모양의 숫자 배열입니다

    1
   1 1
  1 2 1
 1 3 3 1
1 4 6 4 1

이 삼각형의 각 행은 $(x+y)^n$의 전개식에서 나타나는 계수와 일치합니다. 예를 들어

• $(x+y)^0 = 1$ (계수: 1)
• $(x+y)^1 = x + y$ (계수: 1, 1)
• $(x+y)^2 = x^2 + 2xy + y^2$ (계수: 1, 2, 1)
• $(x+y)^3 = x^3 + 3x^2y + 3xy^2 + y^3$ (계수: 1, 3, 3, 1)
• $(x+y)^4 = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4$ (계수: 1, 4, 6, 4, 1)

 

이것을 일반화하면 다음과 같은 이항정리가 됩니다

$$(x+y)^n = \sum_{k=0}^{n} \binom{n}{k} x^{n-k} y^k$$

여기서 $\binom{n}{k}$는 이항계수입니다.

 

다항계수: 이항계수의 확장

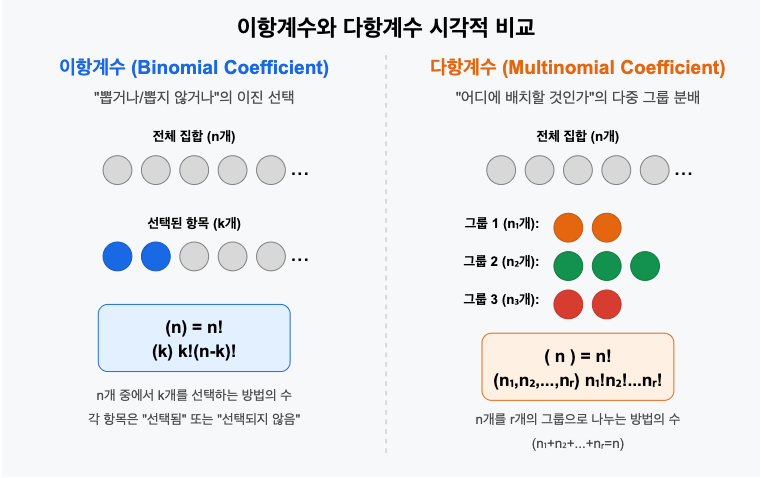
이항계수가 n개의 객체를 두 그룹(선택됨/선택되지 않음)으로 나누는 방법을 계산한다면,

다항계수는 n개의 객체를 r개의 서로 다른 그룹으로 나누는 방법의 수를 계산합니다.

예를 들어, 포커 게임에서 두 사람에게 각각 5장씩 카드를 나누어 주는 방법의 수는 다항계수를 이용해 계산할 수 있습니다.

방법 1: 순차적 접근

두 플레이어에게 순서대로 카드를 나누어 준다고 생각해 봅시다.

1. 첫 번째 플레이어에게 5장을 나누어 주는 방법의 수
   • 52장 중에서 5장을 선택하는 조합의 수
   • $\binom{52}{5} = \frac{52!}{5!(52-5)!} = \frac{52!}{5!47!} \approx 2,598,960$가지
2. 이제 남은 47장 중에서 두 번째 플레이어에게 5장을 나누어 주는 방법의 수
   • $\binom{47}{5} = \frac{47!}{5!(47-5)!} = \frac{47!}{5!42!} \approx 1,533,939$가지

총 경우의 수는 이 두 값을 곱한 것입니다: $\binom{52}{5} \times \binom{47}{5} = \frac{52!}{5!47!} \times \frac{47!}{5!42!} = \frac{52!}{5!5!42!} \approx 3.99 \times 10^{12}$가지

방법 2: 다항계수 활용

더 직접적인 방법으로, 52장의 카드를 세 그룹으로 나누는 상황으로 생각할 수 있습니다

• 첫 번째 플레이어가 받는 5장
• 두 번째 플레이어가 받는 5장
• 남는 42장

이때 다항계수를 사용합니다: $\binom{52}{5,5,42} = \frac{52!}{5!5!42!} \approx 3.99 \times 10^{12}$가지

방법 3 : 범위를 줄이고 나누어주기 

"52장에서 10장을 먼저 선택한 후(첫 번째와 두 번째 플레이어에게 줄 카드), 그 10장을 두 플레이어에게 5장씩 나누는 방법"

이를 수식으로 표현하면: $\binom{52}{10} \times \binom{10}{5} = \frac{52!}{10!42!} \times \frac{10!}{5!5!} = \frac{52!}{5!5!42!}$

여기서 $\binom{10}{5}$는 10장을 두 명에게 각각 5장씩 나누는 방법의 수입니다. 이 접근법도 당연히 같은 결과를 제공합니다.

간단하게 설명하면, 52장의 카드에서 두 사람에게 각각 5장씩 나누어 주는 방법은 약 4조 가지나 되는 엄청난 수입니다. 

다항계수 공식

n개의 객체를 크기가 $n_1, n_2, ..., n_r$인 r개의 그룹으로 나누는 방법의 수는 다음과 같이 계산합니다

$$\binom{n}{n_1, n_2, ..., n_r} = \frac{n!}{n_1! \times n_2! \times ... \times n_r!}$$

이 공식은 다음 조건을 가정합니다

• 모든 객체가 사용됨: $n_1 + n_2 + ... + n_r = n$
• 순서는 중요하지 않음

다항계수 공식의 증명

1. 먼저 $n_1$개의 객체를 선택합니다: $\binom{n}{n_1}$ 가지 방법
2. 남은 객체 중에서 $n_2$개를 선택합니다: $\binom{n-n_1}{n_2}$ 가지 방법
3. 이어서 $n_3$개를 선택합니다: $\binom{n-n_1-n_2}{n_3}$ 가지 방법
4. 이런 방식으로 계속해서 모든 그룹을 선택합니다

이 모든 방법의 수를 곱하면

$$\binom{n}{n_1} \times \binom{n-n_1}{n_2} \times \binom{n-n_1-n_2}{n_3} \times ... $$

이것을 공식으로 전개하고 정리하면:

$$\frac{n!}{n_1!(n-n_1)!} \times \frac{(n-n_1)!}{n_2!(n-n_1-n_2)!} \times \frac{(n-n_1-n_2)!}{n_3!(n-n_1-n_2-n_3)!} \times ...$$

여기서 팩토리얼 항들이 서로 상쇄되면서 최종적으로 다음과 같은 결과가 나옵니다

$$\frac{n!}{n_1! \times n_2! \times ... \times n_r!}$$

다항계수는 다양한 확률 문제에 응용할 수 있습니다

1. 카드 게임: 여러 플레이어에게 카드를 나누어 주는 방법의 수 예: 4명이 각각 13장씩 카드를 받는 방법의 수는 $\binom{52}{13,13,13,13}$
2. 위원회 구성: 여러 개의 소위원회 형성 예: 7명을 2명, 3명, 2명으로 구성된 세 개의 소위원회로 나누는 방법의 수는 $\binom{7}{2,3,2}$
3. 품질 관리: 좋은 제품과 불량 제품의 분류 예: 공장에서 생산된 100개 제품 중 불량품이 10개일 확률 계산
4. 짝짓기 문제: 2n명을 n쌍으로 나누는 방법의 수