곱셈 법칙과 전체 확률의 법칙

곱셈 법칙 (Multiplication Law )

조건부 확률은 P(A|B)를 다음과 같이 정의  됩니다. 

P(A|B) = P(A ∩ B) / P(B)

위의 식에서 P(B)를 양변에 곱하면 다음과 같은 중요한 결과를 얻을 수 있습니다. 

P(A ∩ B) = P(A|B) × P(B)

이것이 바로 곱셈 법칙(Multiplication Law)입니다. 매우 간단해 보이지만, 확률 문제에서 굉장히 자주 사용되는 중요한 법칙입니다.

이 법칙의 직관적인 의미는 무엇일까요? "A와 B가 모두 일어날 확률"은 "B가 일어날 확률"과 "B가 일어났을 때 A가 일어날 확률"의 곱으로 표현할 수 있다는 것입니다. 다시 말해, 두 사건이 모두 일어나려면

1. 먼저 B가 일어나야 하고 (확률 P(B))
2. 그 다음으로 A도 일어나야 합니다 (조건부 확률 P(A|B))

물론, 이 공식은 대칭적이므로 P(A ∩ B) = P(B|A) × P(A)로도 쓸 수 있습니다.

전체 확률의 법칙 (Law of Total Probability)

이제 두 번째 중요한 법칙인 전체 확률의 법칙에 대해 알아봅시다. 이 법칙을 이해하기 위해, 먼저 표본공간 Ω를 서로 겹치지 않는(서로소) 부분집합들로 나눈다고 생각해 봅시다.

예를 들어, Ω = B₁ ∪ B₂ ∪ B₃ ∪ ... ∪ Bₙ이라고 합시다. 여기서 중요한 점은

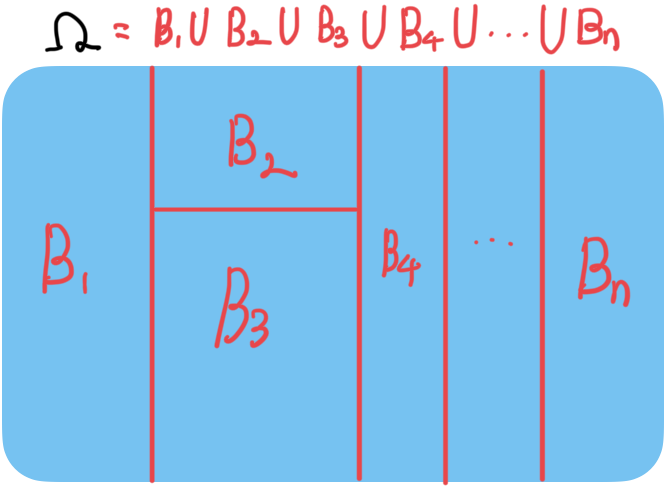
1. 모든 가능한 결과는 이 부분집합들 중 하나에 속합니다 (합집합이 Ω).
2. 각 부분집합은 서로 겹치지 않습니다 (Bᵢ ∩ Bⱼ = ∅, i ≠ j).

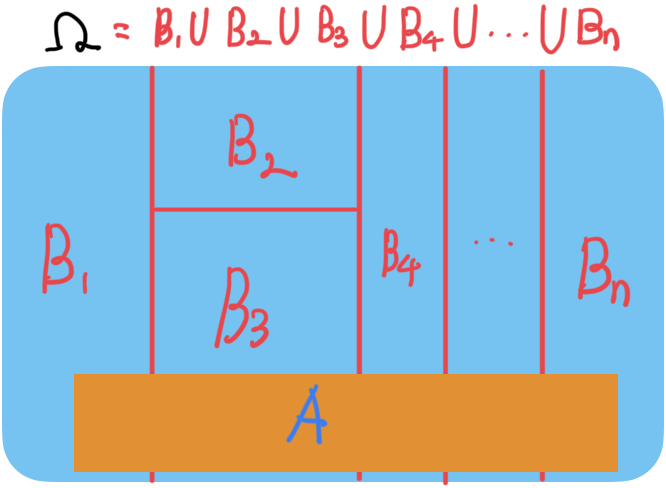
이때 어떤 사건 A의 확률은 다음과 같이 계산할 수 있습니다.

P(A) = P(A|B₁) × P(B₁) + P(A|B₂) × P(B₂) + ... + P(A|Bₙ) × P(Bₙ)

수학적 표기로는: P(A) = Σ P(A|Bᵢ) × P(Bᵢ) ( i = 1부터 n까지 )

이 법칙이 의미하는 바는 무엇일까요? 쉽게 이해하기 위해, 표본공간을 여러 구역으로 나누었다고 생각해 봅시다.

어떤 사건 A가 일어날 전체 확률을 구하려면, 각 구역에서 A가 일어날 조건부 확률을 해당 구역의 크기(확률)와 곱한 후, 이 값들을 모두 더하면 됩니다.

이분법(B와 B의 여집합)

전체 확률의 법칙에서 가장 많이 사용되는 특별한 경우는 표본공간을 단 두 개의 부분집합으로 나누는 경우입니다.

즉, 어떤 사건 B와 그것의 여집합 Bᶜ(B가 일어나지 않는 경우)로 나누는 것입니다.

이 경우, 전체 확률의 법칙은 다음과 같이 단순화됩니다

P(A) = P(A|B) × P(B) + P(A|Bᶜ) × P(Bᶜ)

이것은 "A가 일어날 확률은 B가 일어났을 때 A가 일어날 확률과 B가 일어나지 않았을 때 A가 일어날 확률의 가중 평균이다"라고 해석할 수 있습니다. 여기서 가중치는 각각 P(B)와 P(Bᶜ) = 1 - P(B)입니다.

카드 게임 예시로 이해하기

전체 확률의 법칙을 카드 게임 예시로 이해해 봅시다.

표준 52장 카드에서 한 장을 뽑을 때, 빨간 카드가 나올 확률 P(A)을 구해봅시다. 여기서 A는 "카드가 빨간색"인 사건입니다.

우리는 표본공간을 4개의 서로소 부분집합으로 나눌 수 있습니다:

• B₁: 카드가 하트인 경우
• B₂: 카드가 다이아몬드인 경우
• B₃: 카드가 클럽인 경우
• B₄: 카드가 스페이드인 경우

 

각 부분집합의 확률은 P(B₁) = P(B₂) = P(B₃) = P(B₄) = 1/4입니다.

 

이제 전체 확률의 법칙을 적용해 봅시다

P(A) = P(A|B₁) × P(B₁) + P(A|B₂) × P(B₂) + P(A|B₃) × P(B₃) + P(A|B₄) × P(B₄)

• P(A|B₁) = 1 (하트는 빨간색이므로, 하트가 나왔을 때 빨간 카드가 나올 확률은 100%)
• P(A|B₂) = 1 (다이아몬드도 빨간색)
• P(A|B₃) = 0 (클럽은 검은색)
• P(A|B₄) = 0 (스페이드도 검은색)

 

따라서 P(A) = 1 × (1/4) + 1 × (1/4) + 0 × (1/4) + 0 × (1/4) = 1/4 + 1/4 = 1/2

즉, 카드가 빨간색일 확률은 1/2 또는 50%입니다. 이는 우리가 직관적으로 아는 것과 일치합니다.

정리

1. 곱셈 법칙: P(A ∩ B) = P(A|B) × P(B)
   • 두 사건이 모두 일어날 확률은 한 사건이 일어났을 때 다른 사건이 일어날 조건부 확률과 첫 번째 사건의 확률의 곱입니다.
2. 전체 확률의 법칙: P(A) = Σ P(A|Bᵢ) × P(Bᵢ)
   • 사건 A의 확률은 표본공간을 분할하는 각 부분집합에서의 조건부 확률을 해당 부분집합의 확률로 가중평균한 값입니다.