부분게임 완전균형

완비정보하에서의 동태적 게임

경기자들이 모두 게임의 구조(전략,보수)를 알고 있는상태에서 순차적으로 전략을 선택하는 형태의 게임을 의미한다. 

 

 

순차적 게임에서의 전략집합

순차적게임(동태적게임)에서의 전략집합은 각 경기자들이 자신들이 위치한 노드에서 가능한 전략을 모은 것이다.

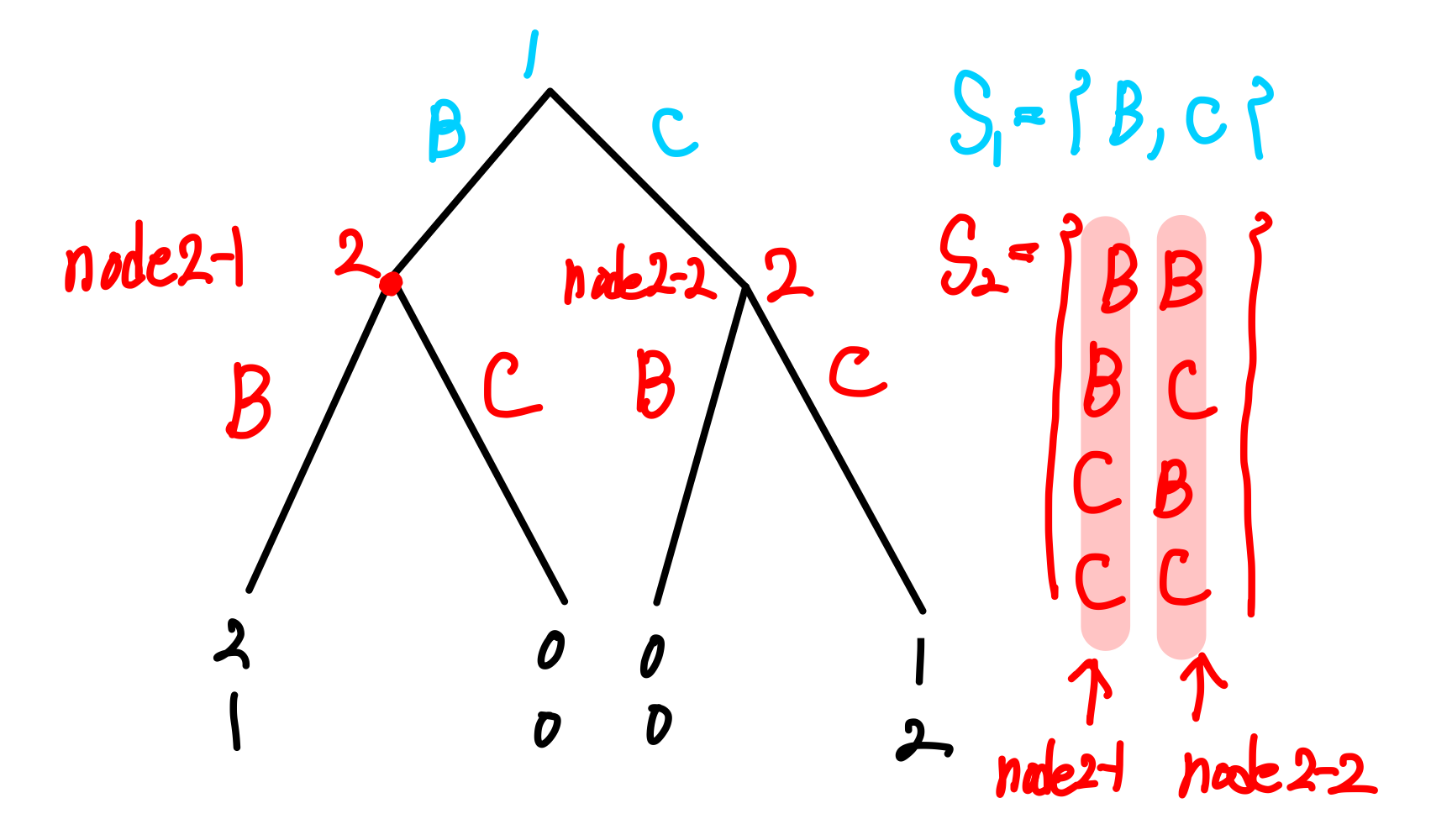
위에서 나타난 동태적 게임은 경기자 1이 먼저 전략을 선택하고, 이후 경기자 2가 전략을 선택한다.

경기자 1의 노드는 1개로 가능한 전략집합은 노드1에서의 B 또는 C이다.

경기자 2의 노드는 2개로 가능한 전략집합은 노드2-1에서의 B,C와 노드 2-2에서의 B,C의 조합으로 BB,BC,CB,CC이다.

 

진입게임의 내쉬균형

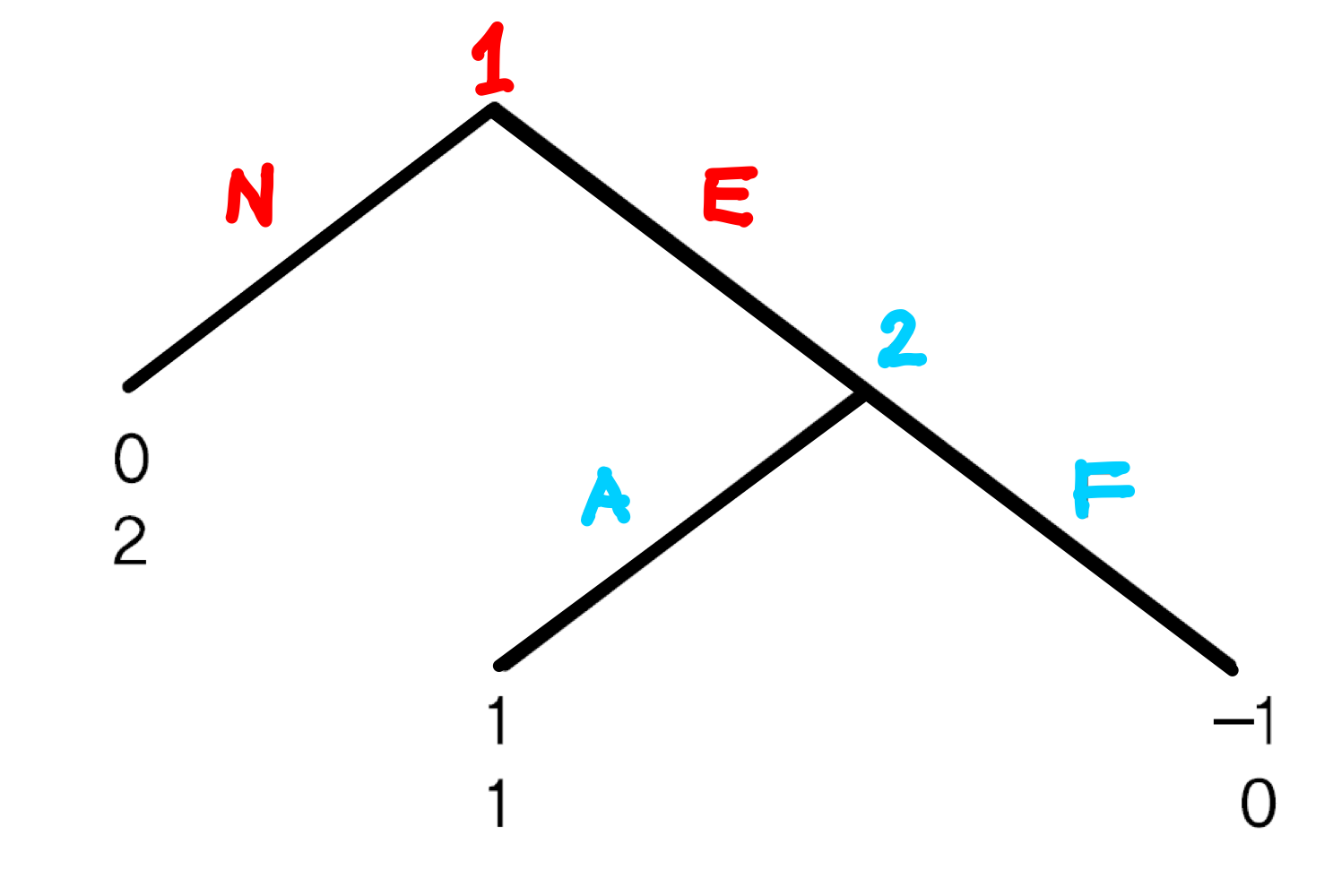
진입게임을 보수행렬로 나타내면 아래와 같다. 

보수행렬을 이용해 이 게임의 내쉬균형을 도출하면 두개의 내쉬균형 (E,A)와 (N,F)가 도출된다.

(N,F)는 경기자들이 합리적인 선택을 할 것이라고 가정했을 때 도달할 수 없는 균형이다. 

때문에 이러한 도달할수 없는 균형을 걸러낼수 있는 방법이 필요하다.

 

균형에서의 도달 여부와 관계없이 모든 부분게임에서 경기자들이 합리적인 행동할것을 요구한다. 

 

부분게임이란?

부분게임은 게임을 구성하고 있는 일부로서 해당 부분만 독립적으로 떼어내어 별도의 게임으로 해석할 수 있는 부분을 말한다.

1. 하나의 결정마디로 시작한다.-> 노드 하나로부터 뻗어나온다.

2. 시작 결정마디와 그 뒤에 등장하는 모든 결정마디 및 보수로 구성된다. -> 게임의 요소를 모두 갖추고 있다.

3. 정보집합을 자르지 않는다. -> 정보집합이 잘리게 되면 경기자가 어느 노드에 위치해있는지 알지 못한다.(독립성의 상실)

 

 

부분게임완전균형 (Subgame Perpect Nash Equilibrium,SPNE)

경지자들이 모든 부분게임에서 최적의 선택을 하는 내쉬균형

-> 모든부분게임에 대해서도 내쉬균형이 달성되도록 하는 전략명세를 의미한다.

 

역진귀납 (Backward Induction)

완비정보하에서의 게임이기 때문에 각 경기자들은 내가 어떠한 전략을 선택했을 때 상대의 대응을 알 수 있다.

때문에 그 대응을 사전에 고려해서 전략을 선택을 할 수 있다. 

 

게임트리의 바닥에 있는 부분게임의 각 노드에서 경기자들의 최적대응을 고려하면 어떤 노드로 가는 선택을 해야 선선택자가 효용을 최대화 할 수 있는지 알 수 있다.   -> 먼저 선택을 하는 경기자는 상대에게 전략을 선택시킬 수 있다. 

 

역진귀납법을 이용해서 SPNE 도출하기

트리의 바닥에서부터 시작해서 각 부분게임의 노드에 위치한 경기자들의 최적대응을 고려한다.

 

node1-2: 경기자 1은 효용이 더 큰 전략 R을 선택할 것이다.

node1-3: 경기자 1은 효용이 더 큰 전략 L을 선택할 것이다.

 

위에서 언급한 내용은 완비정보하에서 경기자 2도 알고 있다. 

때문에 ​node1-2-R과 node1-3-L을 비교하여 경기자 2의 효용이 더 큰 node1-2-R을 선택한다.

node1-2에 도달하기 위해서 2는 A를 선택한다.

 

위에서 언급한 내용 또한 완비정보하에서 경기자 1도 알고 있다.

즉 경기자 2가 A를 선택할 것을 알고 있으며 그 때 자신이 R을 선택하여 효용 5를 얻을 것을 알고 있다.

때문에 경기자 1은 node1-1-L과 node1-2-R을 비교한다.

node1-2-R의 효용이 더 크기 때문에 경기자 1은 node1-1에서 R을 선택한다.

 

SPNE는 경기자들이 각 노드에서 선택할 전략의 집합이다. 위의 역진귀납법을 통한 분석을 이용하여 도출하면 다음과 같다.

(RRL,A)

 

도출한 SPNE는 모든 부분게임에 대해서도 합리적인 선택(각 경기자들의 최적대응)을 만족한다.

따라서 게임 전체적으로도 합리적인 균형으로 볼 수 있다.