부동 소수점이란?

컴퓨터가 실수를 표현하는 방식 

10진법 

우리가 일상적으로 수를 사용할 때는 10진수 체계를 사용합니다. 

0부터 9까지 총 10개의 숫자를 사용하며 각 자릿수는 10의 제곱의 형태로 표현합니다.

 

예를 들어 "2025"라는 숫자는 다음과 같이 이해할 수 있습니다. 

2 × 10^3 = 2000

0 × 10^2 = 0

2 × 10^1 = 20

5 × 10^0 = 5

2000 + 0 + 20 + 5 = 2025

2진법

위와 달리 2진법은 0과 1 단 두개의 숫자를 사용하며 각 자릿수는 2의 제곱의 형태로 표현합니다.

 

예를 들어 "1101"라는 숫자는 다음과 같이 계산됩니다. 

• 1 × 2^3 = 8
• 1 × 2^2 = 4
• 0 × 2^1 = 0 
• 1 × 2^0 = 1
• 8 + 4 + 0 + 1 = 13

2진법으로 실수를 표현하는 방법

정수 변환 과정은 나누기를 사용합니다.

2로 계속 나누면서 나머지를 아래에서 위로 읽어가는 방식입니다.

 

예를 들어 13을 2진수로 변환하는 과정을 보겠습니다
13 ÷ 2 = 6 나머지 1
6 ÷ 2 = 3  나머지 0
3 ÷ 2 = 1  나머지 1
1 ÷ 2 = 0  나머지 1

아래에서 위로 나머지를 읽으면 1101(2진수)가 됩니다.

 

반면에 소수 변환 과정은 곱하기를 사용합니다. 

2를 계속 곱하면서 정수부를 위에서 아래로 읽어가는 방식입니다. 

 

예를 들어 0.625를 2진수로 변환하는 과정을 보겠습니다
0.625 × 2 = 1.25  정수부 1
0.25 × 2 = 0.5   정수부 0
0.5 × 2 = 1.0    정수부 1

위에서 아래로 정수부를 읽으면 0.101(2진수)가 됩니다.

 

그러면 실수 7.7를 2진법으로 나타내봅시다. 먼저 7.7를 정수부와 소수부로 나눕니다.  

• 정수부 : 7 
• 소수부: 0.7

그리고 각 부분을 2진법으로 변환합니다.

1.  정수부 (7) 변환 과정 

7 ÷ 2 = 3 나머지 1
3 ÷ 2 = 1 나머지 1
1 ÷ 2 = 0 나머지 1

따라서 7은 2진수로 111이됩니다. 

 

2. 소수부 (0.7) 변환 과정

0.7 × 2 = 1.4  → 1
0.4 × 2 = 0.8  → 0
0.8 × 2 = 1.6  → 1
0.6 × 2 = 1.2  → 1
0.2 × 2 = 0.4  → 0 ...

0.4가 다시 등장했으므로 위의 패턴은 계속 반복될 것입니다. 

0.7은 2진수로 표현하면 0.1011 1011 1011 .... 와 같이 무한히 반복됩니다. 

 

위와 같이 무한히 반복되는 2진수는 어쩔수 없이 표현할 수 있는 가장 근사치의 값으로 저장합니다. 

이 근사치 값을 저장하는 방법으로 고정 소수점 방법이라는게 있습니다. 

 

 

고정 소수점 

 

• 정수를 표현하는 비트수와 소수부를 표현하는 비트수를 밀 정해 두고 해당 비트 만큼만 사용해서 숫자를 표현하는 방식입니다. 
• 예를 들어 실수를 표현하기 위해 4byte(32bit)를 사용하고 그 중 부호를 나타내기 위한 1비트, 그리고 정수에 15비트, 소수에 16비트를 사용하도록 약속해 놓은 시스템이 있으면 해당 시스템에서 7.7은 (0)000000000000 111 . 1011 1011 1011 1011  로 나타낼 수 있습니다. 

고정 소수점 방식을 사용하면 실수의 정수부와 소수부를 나타낼 수 있지만 다음과 같은 단점이 존재합니다. 

 

1. 표현할 수 있는 수의 범위가 제한적입니다. 

2. 정밀도(소수점의 위치)가 고정되어 있어 매우 큰 수나 매우 작은 수를 동시에 다루기 어렵습니다. 

 

정수부를 늘리면 더 큰 숫자를 표현할 수 있지만 정밀한 숫자를 표현하기 어렵습니다. 그렇다고 소수부를 늘리면 더 정밀한 숫자를 표현할 수 있지만 큰 숫자를 표현하지 못합니다.

 

 

부동 소수점

한정된 비트 안에서 정수부와 소수부를 나누어 값을 저장하는 고정 소수점 방식과는 달리 

부동소수점 방식은 숫자를 가수부 지수부로 나누어 표현하는 방식으로

지수부를 통해 소수점의 위치를 바꿈으로써 더 큰 범위의 숫자를 유동적으로 저장할 수 있습니다. 

 

예를 들어, 123.45라는 숫자는 1.2345 × 10² 로 표현할 수 있습니다. 여기서:

• 1.2345는 가수(mantissa) 부분
• 2는 지수(exponent) 부분
• 10은 기수(base)입니다

 

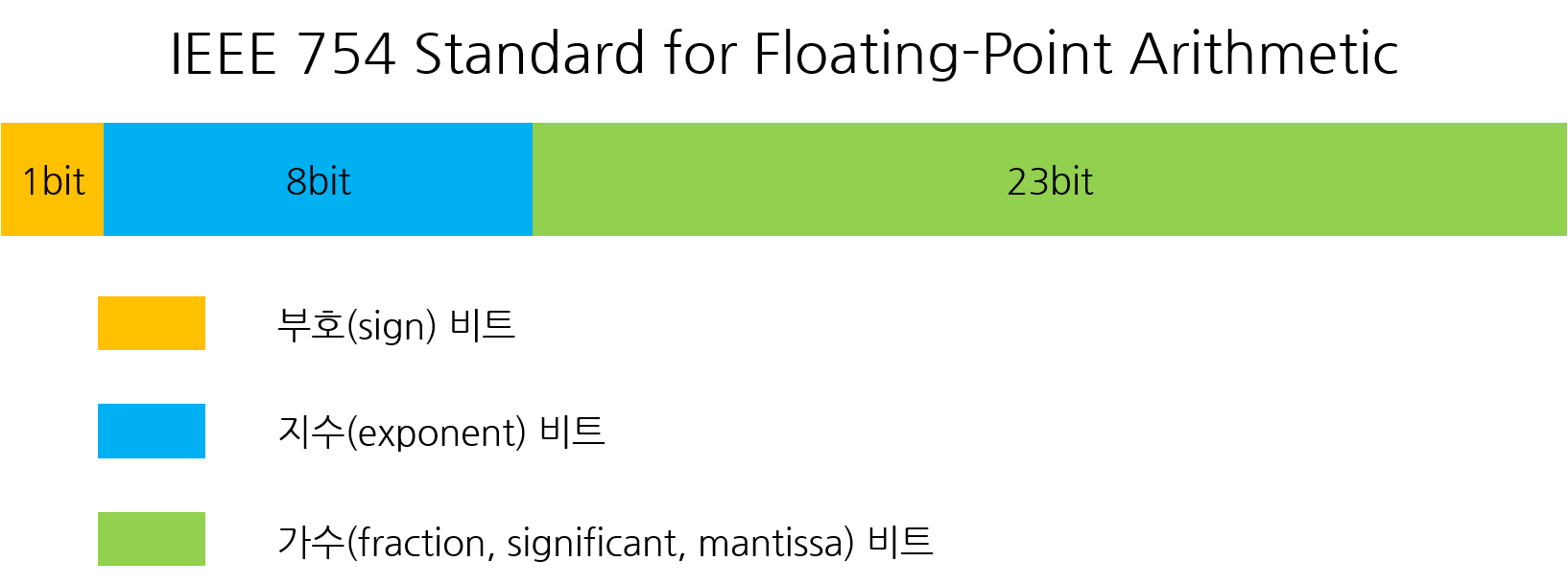
위의 다이어그램은 IEEE 754 단정밀도(32비트) 부동 소수점 형식을 보여줍니다. 

1. 부호 비트(S, Sign bit):
   • 가장 왼쪽의 1비트
   • 0이면 양수, 1이면 음수를 나타냅니다
2. 지수 부분(E, Exponent):
   • 8비트를 사용
   • 편향된(biased) 형식을 사용하여 127을 더한 값을 저장
   • 범위는 -126에서 127까지 표현 가능
3. 가수 부분(M, Mantissa):
   • 23비트를 사용
   • 1.xxxxx 형태에서 소수점 이하 부분만 저장
   • 정규화된 형태에서는 항상 1.xxxxx 형식이므로 1은 암묵적으로 표현

실제 값은 다음 공식으로 계산됩니다: (-1)^S × 2^(E-127) × (1.M)

 

 

고정 소수점 , 부동 소수점 비교

고정 소수점과 부동 소수점의 수 표현 범위 차이를 16비트(2바이트)를 사용하는 경우를 통해 비교할 수 있습니다. 

고정 소수점 방식

16비트로 정수부 8비트, 소수부 8비트를 표현한다고 가정해봅시다

• 8비트 정수부: -128 ~ 127 표현 가능
• 8비트 소수부: 1/256 단위로 표현 가능
• 최대값 = 127.99609375  ( 01111111.11111111 )
• 최소값 = -128.0  ( 10000000.00000000 )
• 정밀도 = 0.00390625    # 0.00000001 (1/256)

 

부동 소수점 방식
이제 같은 16비트로 부동 소수점을 표현해보겠습니다.

1비트는 부호, 5비트는 지수부, 10비트는 가수부로 사용한다고 가정해봅시다

• 1비트 부호: +/-
• 5비트 지수부: -16 ~ 15 표현 가능
• 10비트 가수부: 1024개의 유효숫자 표현 가능
• 최대값 = 65504    ( 2^15 * (1 + 1023/1024) )
• 최소값 = -65504   ( -2^15 * (1 + 1023/1024) )
• 최소정규값 = 6.1035e-5  ( 2^-16 * (1) )

이처럼 부동 소수점은 지수부를 활용하여 소수점의 위치를 자유롭게 이동시킬 수 있기 때문에, 같은 비트 수로도 훨씬 더 넓은 범위의 수를 표현할 수 있습니다. 

 

 

편향된 지수 방식 ( Biased Exponent )

부동 소수점에서 지수를 저장하는 방식으로, 실제 지수 값에 고정된 편향값(bias)를 더해서 저장합니다. 

예를 들어, 실제 지수가 2라면 129(2+127) = 01111100 를 저장하게 됩니다.

 

32비트 단정도 부동소수점에서 지수부는 8비트를 사용합니다. 

 

8비트로 표현할 수 있는 범위는 00000000(0)부터 11111111(255)까지입니다.

그러나 여기서 두 가지 특별한 값을 제외합니다
1. 00000000(0): 0과 비정규화된 수를 표현할 때 사용
2. 11111111(255): 무한대와 NaN(Not a Number)을 표현할 때 사용

따라서 실제 사용 가능한 범위는
- 최솟값: 00000001(1)
- 최댓값: 11111110(254)

편향값(Bias) 적용
편향값 127을 뺐을 때의 실제 지수 범위는
- 최솟값: 1 - 127 = -126
- 최댓값: 254 - 127 = +127

 

편향된 지수 방식을 사용하는 이유

1. 모든 지수값이 양수로 저장되므로 수의 크기 비교가 매우 단순해집니다. 일반적인 정수 비교처럼 저장된 값을 직접 비교할 수 있기 때문입니다.
2. 2의 보수 방식과 달리 부호 비트를 따로 처리할 필요가 없어 하드웨어 구현이 간단해집니다.

 

정규화 ( Normalization ) 

정규화는 부동소수점 수를 표현할 때 가수부를 항상 1.xxx 형태로 만드는 과정입니다.

정규화의 가장 큰 특징은 정수부의 1이 항상 존재한다는 것을 알고 있으므로, 이를 암묵적으로 표현한다는 점입니다.

이를 '숨겨진 1비트(hidden one bit)'라고 부릅니다.

이를 통해 23비트의 가수부로 실제로는 24비트의 정밀도를 얻을 수 있습니다.

 

십진수 12.34를 이진 부동소수점으로 변환
1. 이진수 변환: 1100.01011...
2. 정규화: 1.10001011... × 2³
3. 저장: 가수부에는 10001011...만 저장 (앞의 1은 암묵적)

 

 

고정 소수점과 부동 소수점 활용 

고정 소수점이 사용되는 경우

금융 

은행의 계좌 잔고나 주식 거래 시스템에서는 고정 소수점 방식을 선호합니다. 예를 들어, 통화를 다룰 때는 보통 소수점 둘째 자리까지만 필요하며, 정확한 값이 중요합니다. $10.25에서 $0.01을 뺐을 때 정확히 $10.24가 나와야 하죠. 부동 소수점을 사용하면 0.01같은 숫자를 정확히 표현할 수 없어 미세한 오차가 발생할 수 있습니다.

임베디드 시스템

에서도 고정 소수점이 자주 사용됩니다. 예를 들어, 간단한 온도 제어 시스템에서 -40.00°C에서 +100.00°C 정도의 범위만 다룬다면, 고정 소수점으로 충분합니다. 더구나 고정 소수점 연산은 단순하여 처리 속도가 빠르고, 제한된 하드웨어 자원을 효율적으로 사용할 수 있습니다.

부동 소수점이 사용되는 경우

3D 그래픽스 분야

게임에서 카메라가 매우 먼 산도 보고, 캐릭터 손의 미세한 움직임도 표현해야 한다고 생각해보세요. 산까지의 거리는 수천 단위가 될 수 있고, 손가락 움직임은 0.001 단위로 정밀해야 할 수 있습니다. 부동 소수점은 이런 다양한 스케일의 수를 효율적으로 다룰 수 있습니다.

과학 계산

우주의 거리(광년 단위)부터 원자 크기(나노미터 단위)까지 다뤄야 하는 경우, 부동 소수점의 넓은 범위가 필수적입니다. 게다가 과학 계산에서는 대개 상대적 오차가 중요한데, 부동 소수점은 이를 자연스럽게 지원합니다.

 

정확성이 절대적으로 중요하고 범위가 제한적이라면 고정 소수점을, 넓은 범위의 수를 다루거나 상대적 정밀도가 중요하다면 부동 소수점을 선택하는 것이 바람직합니다.

 

참고 자료

부동 소수점(Floating Point)란 무엇인가? — Steemit