유한차분법

수치해석적 미분이 필요한 이유?

실험을 통한 측정이나 관측을 이용하여 얻은 데이터들은 이산적이기 때문에 해석적으로 미분이 불가한 경우가 많다.

따라서 수치적 해석을 함으로서 데이터의 독립변수 대비 종속변수의 변화 경향성을 알 수 있다.

---

수치해석적 미분 접근방법

1. 인접한 점들을 선으로 연결함으로서 기울기를 구하는 방법(유한차분법)

2. Curve-fitting을 이용하여 데이터에 들어맞는 함수식을 찾은 뒤 해석적으로 미분하는 방법

---

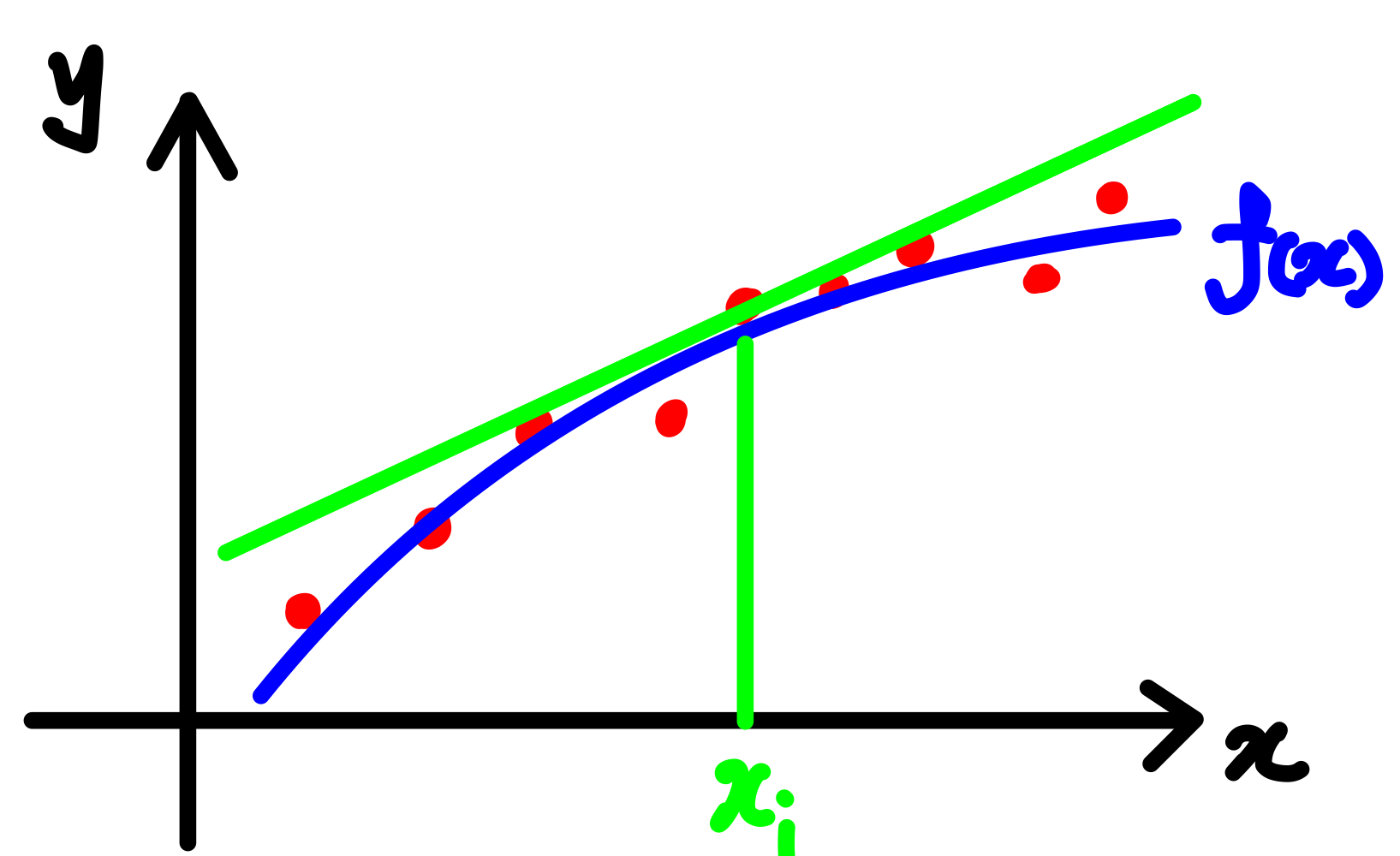
수치해석적 미분시 고려해야 할 점

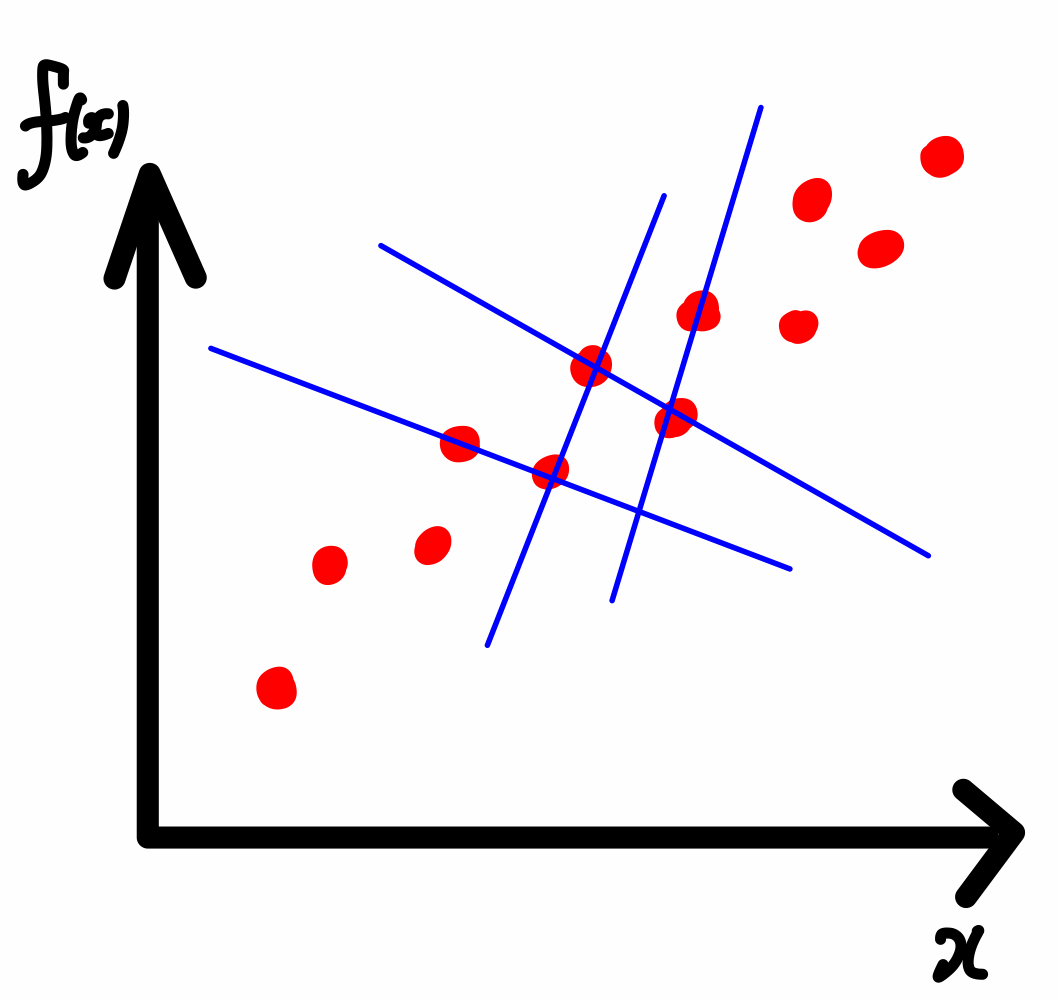
전체적으로 봤을 때는 $x$가 증가함에 따라서 $y$가 증가하는 모습을 확인할 수 있다.

하지만 인접한 두점을 이을 경우 계속해서 기울기가 양의 값과 음의 값으로 변동이 심한 것을 볼 수 있다.

위처럼 실험이나 관측을 통해 얻은 데이터들은 측정오류나 데이터 자체의 불확실성을 가지고 있다.

따라서 이 경우에는 인접한 두점이 아닌 더 많은 점을 가지고 데이터의 경향성을 파악해야한다.

즉 얻은 데이터에 포함되어 있는 오차나 변동을 항상 고려해주어야한다. 

 

---

미분의 유한차분 근사법

미분값을 구하려는 점 $a$와 임의의 $x$의 함수값과 떨어진 거리를 이용하여 기울기 값을 얻는다.

이때 $x$를 $a$쪽으로 가깝게 접근시킴으로서 둘사이의 기울기 값을  점 $a$에서의 미분값에 근사시킬 수 있다.

 

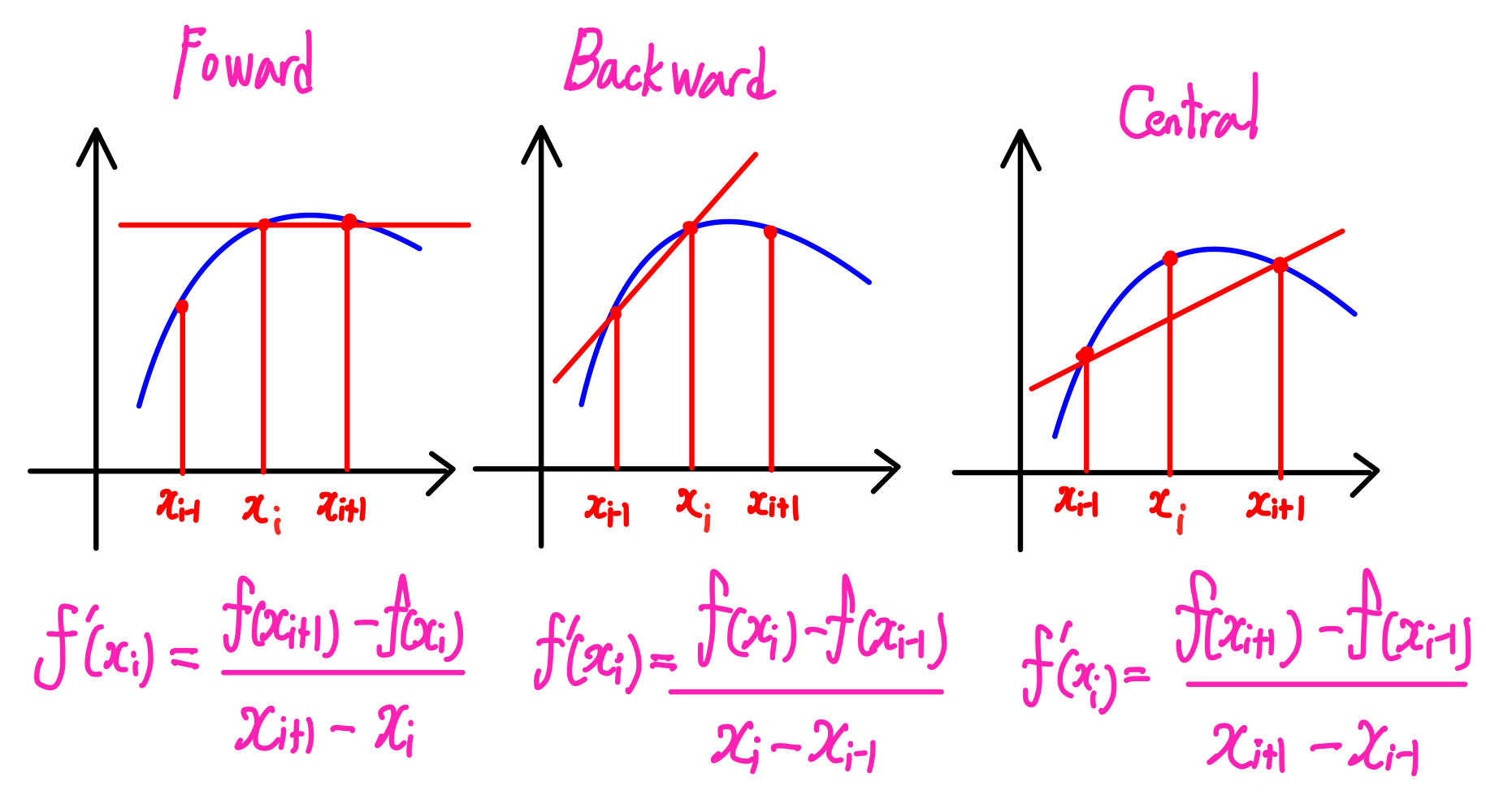
미분값에 근사시킬 기울기를 구할 때 사용하는 점에 따라서 전방차분법,후방차분법,중앙차분법으로 구분된다.

---

테일러급수

주어진 점 $a$에서의 함수값과 그 주변에서의 변화경향성(미분값)을 알때

해당 점에서 $\Delta x$ 만큼 떨어진 곳에서의 함수값을 근사시켜 구할 수 있다.

 

 

 

유한차분법 테일러급수로 전개

 

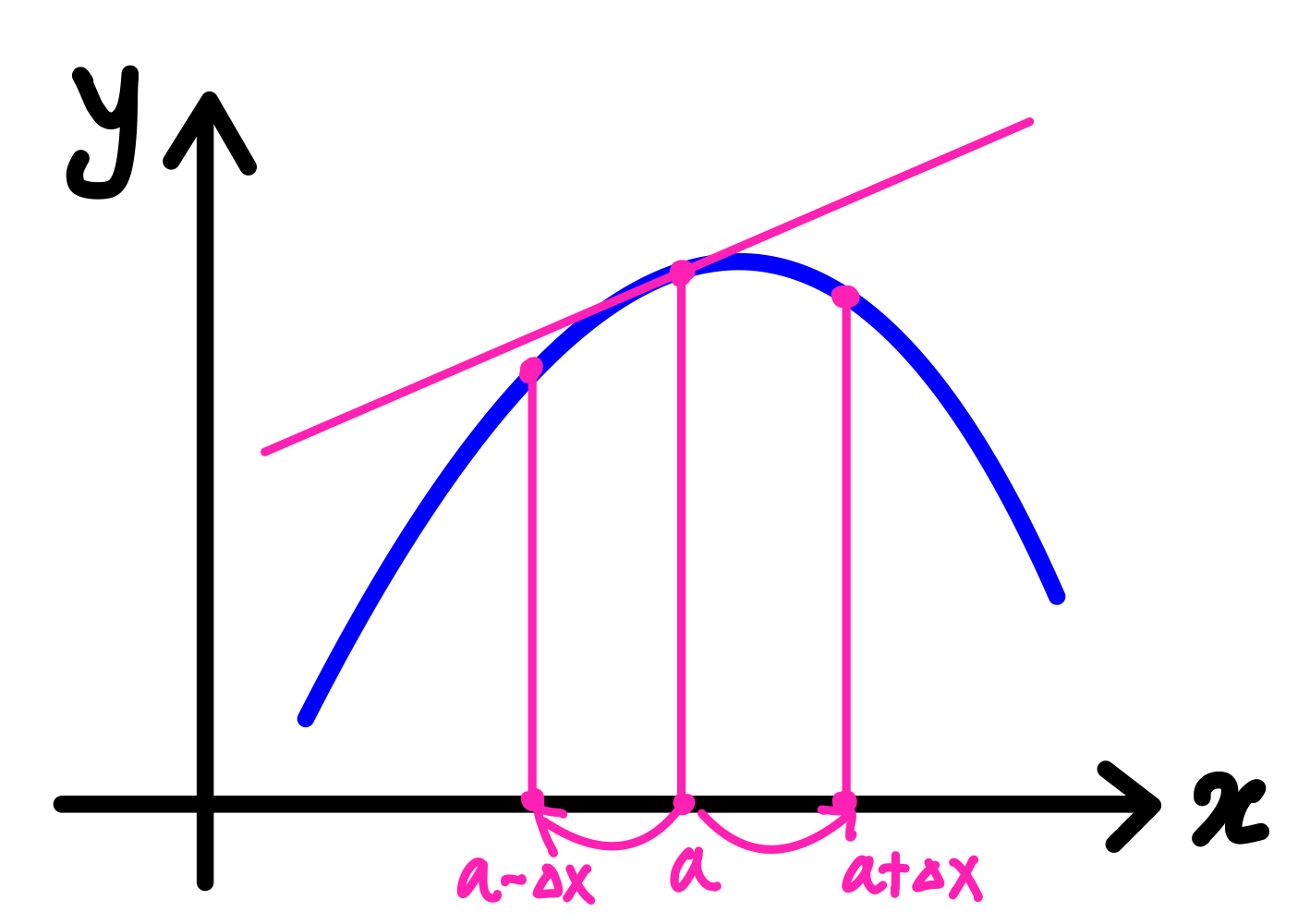
1계도함수

 

전방차분법

후방차분법

중앙차분법

중앙차분법은 전방이나 후방차분법에 비해 Error terms의 변수가 $\Delta x^2$으로 $\Delta x$에 비해 Error terms이 작은 것을 알 수 있다. 즉 중앙차분법이 테일러 전개로 인한 오차가 더 적으므로 더 정확하다. 

 

전방차분법과 후방차분법의 정확도를 올리는 방법

전방차분법과 후방차분법은 미분값을 얻으려는 점을 기준으로 한쪽 방향만 고려하는 것과 달리 중앙 차분법은 양쪽 방향을 모두 고려하기 때문에 더 높은 정확도를 가진다. 전방차분법과 후방차분법가 더 높은 정확도를 가지기위해서는 더 많은 데이터점을 고려하면 된다.

 

---

위의 방법과 같이 미분하려는 점 앞의 두점을 적절히 조합하면 전방차분법을 이용한 미분값의 오류항의 작아짐을 볼 수 있다. 

위의 방법을 후방차분법에도 똑같이 적용하면 아래와 같은 식을 얻을 수 있다.

 

---

2계도 함수

전방차분법과 후방차분법을 조합하여 2차도함수를 얻을 수 있다.

---

오차에 관하여

1. 테일러 급수 전개로 인한 절단 오차

테일러급수를 이용할 때 모든 항을 고려할 수 없기 때문에 고차항들은 제외함으로서 나오는 오차이다. 

고차항에 곱해진 $\Delta x$ 중에 가장 차수가 작은 항을 고려한다. 왜냐하면 $\Delta x$가 1미만이기 때문에 차수가 작을수록 절단오차에서 대부분의 비중을 차지하기 때문이다.

 

2. 컴퓨터 연산으로 인한 Machine Error

- Machine Precision

컴퓨터가 연산시 구분할 수 있는 수의 차이를 의미한다. 

만약에 컴퓨터의 Machine Precision $\epsilon=10^{-16}$라 하면 이 컴퓨터에게 더 작은 차이인 $\epsilon=10^{17}$은 무시된다.

즉 $5+10^{-17}$는 5와 완전히 같은 숫자로 인식된다. 이로 인해 무시된 수에 의해 발생되는 오차를 Machine Error라고 한다.

위에 식에서 볼 수 있듯이 $\Delta x$가 작아짐에 따라서 절단오차 $Q(\Delta x)$는 감소하고 Machine Error $\frac{\epsilon}{\Delta x}$는 증가한다. 두가지 오차가 상충관계에 놓여 있으므로 이사이의 절충이 필요하다.

---