-
라플라스 변환은 푸리에 변환의 일반형이다.Math♾️/Fourier Analysis 2022. 9. 23. 22:07
푸리에 변환
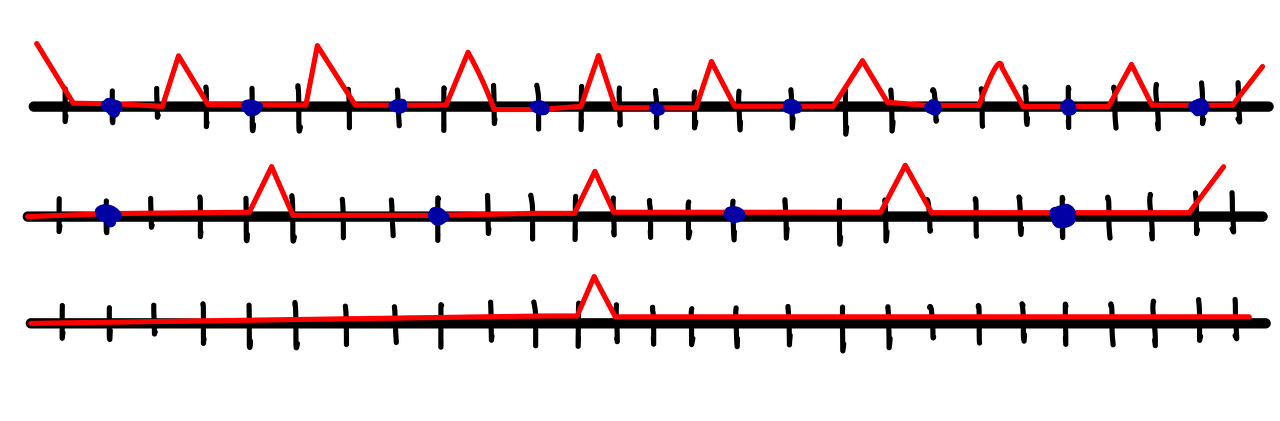
푸리에 변환은 주기 함수의 주기를 무한대로 함으로써 파형의 주기성을 제거하고 파형자체만 남겼다.
이를 진동수 축에 사영시킴으로써 시간에 대하여 나타나던 파형을 진동수에 대해 나타낼 수 있었다.
푸리에 변환을 하기 위해서는 대상이 되는 함수가 주기를 가지고 있어야한다. (하나의 구간에 파형의 전체가 나타나야한다.)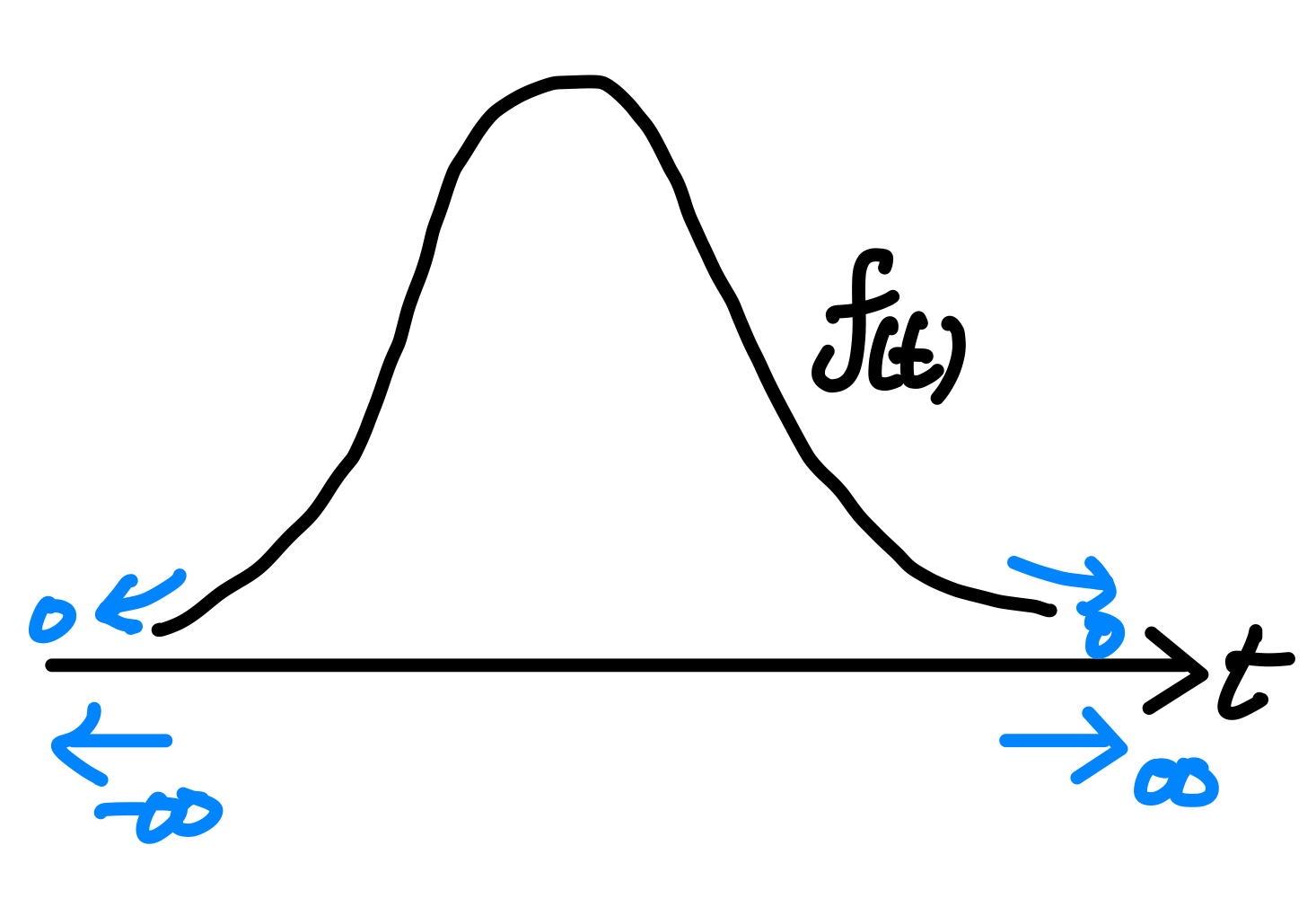
주기를 가진 함수는 주기를 무한대로 보내어 하나의 구간에 대해서 확대되어 나타내면 양쪽값이 0에 수렴한다.
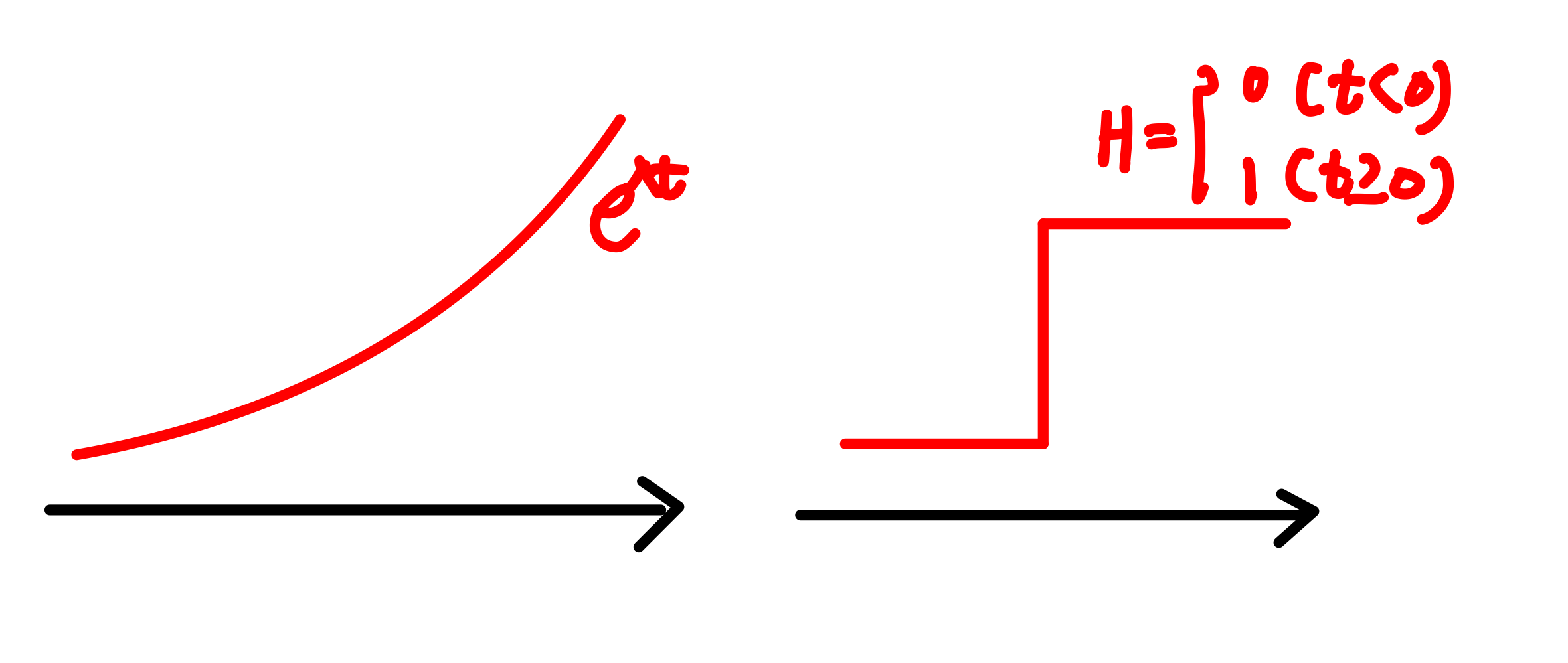
하지만 주기함수가 아닌 일반적인 함수에서 양쪽 값 모두 0에 수렴하지 않는 경우에 푸리에 변환을 적용할 수 가 없다.
라플라스 변환
라플라스 변환은 푸리에 변환을 적용할 수 없는 함수에 대하여 푸리에 변환을 가능하게 한 방법이다.
Heaviside 계단 함수를 예로 들면 아래와 같다.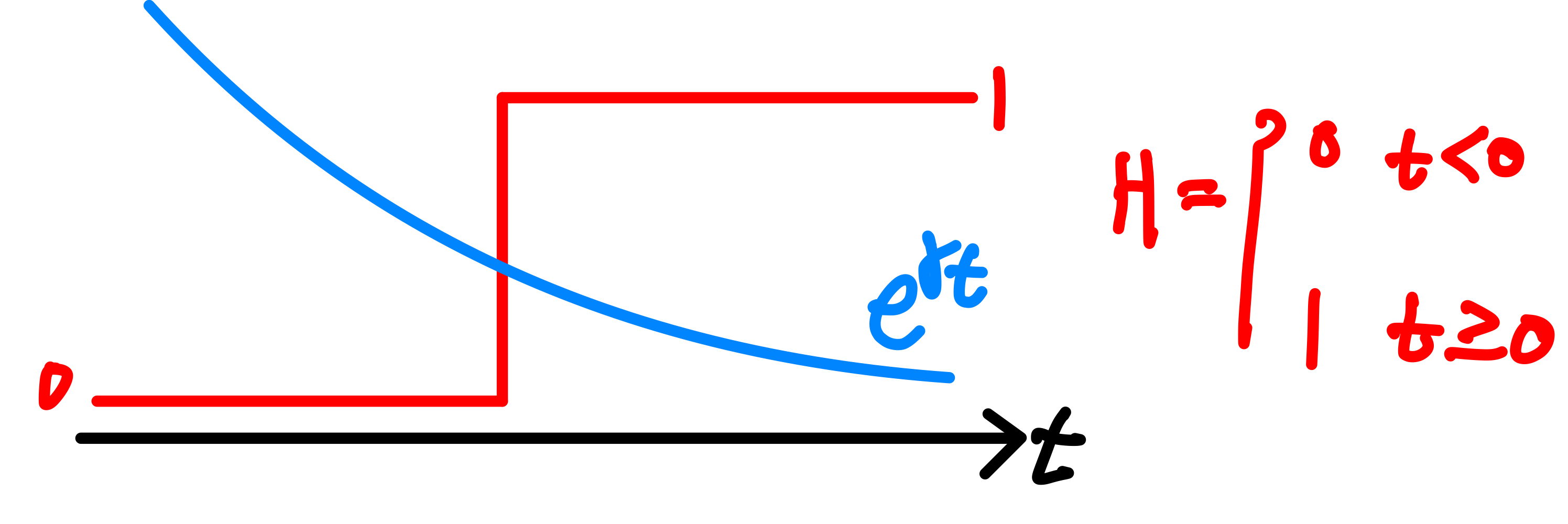
Heaviside 계단 함수에 $e^{\gamma t}$를 곱하여 0에 붙지 않는 쪽을 0에 수렴 시키도록 하는 것이다.
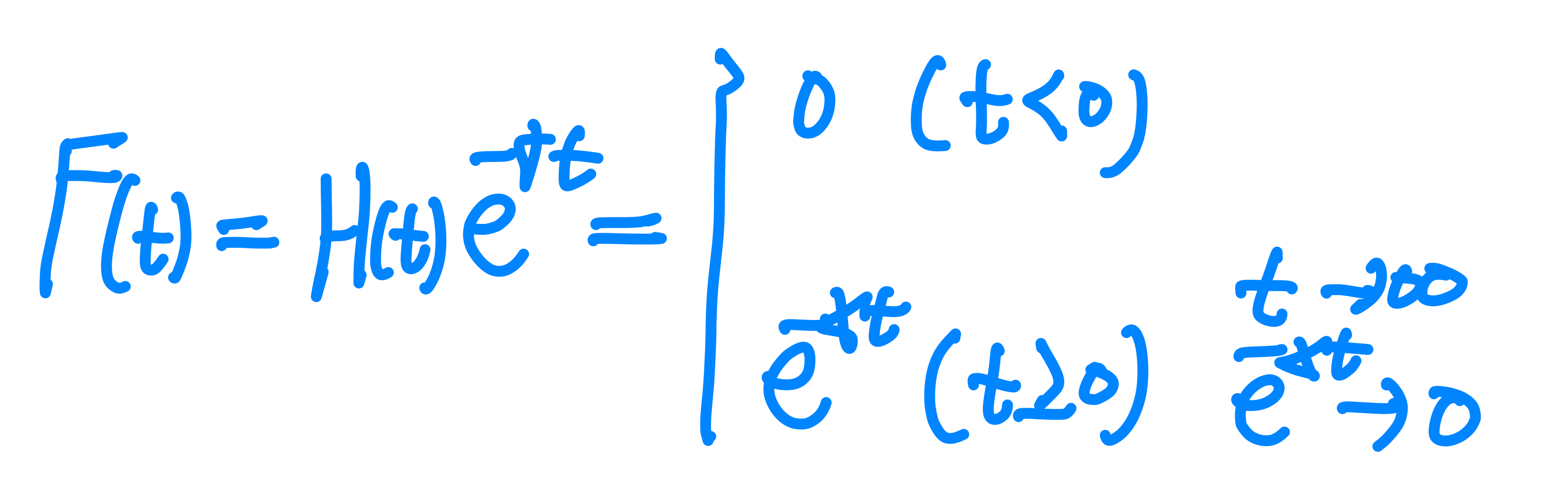

$e^{\gamma t}$를 곱하여 양쪽을 모두 0에 수렴시켜 푸리에 변환이 가능해진 새로운 함수 $F(t)=f(t)e^{\gamma t}$에 대해서 푸리에 변환을 하는 것이다.
- 라플라스 변환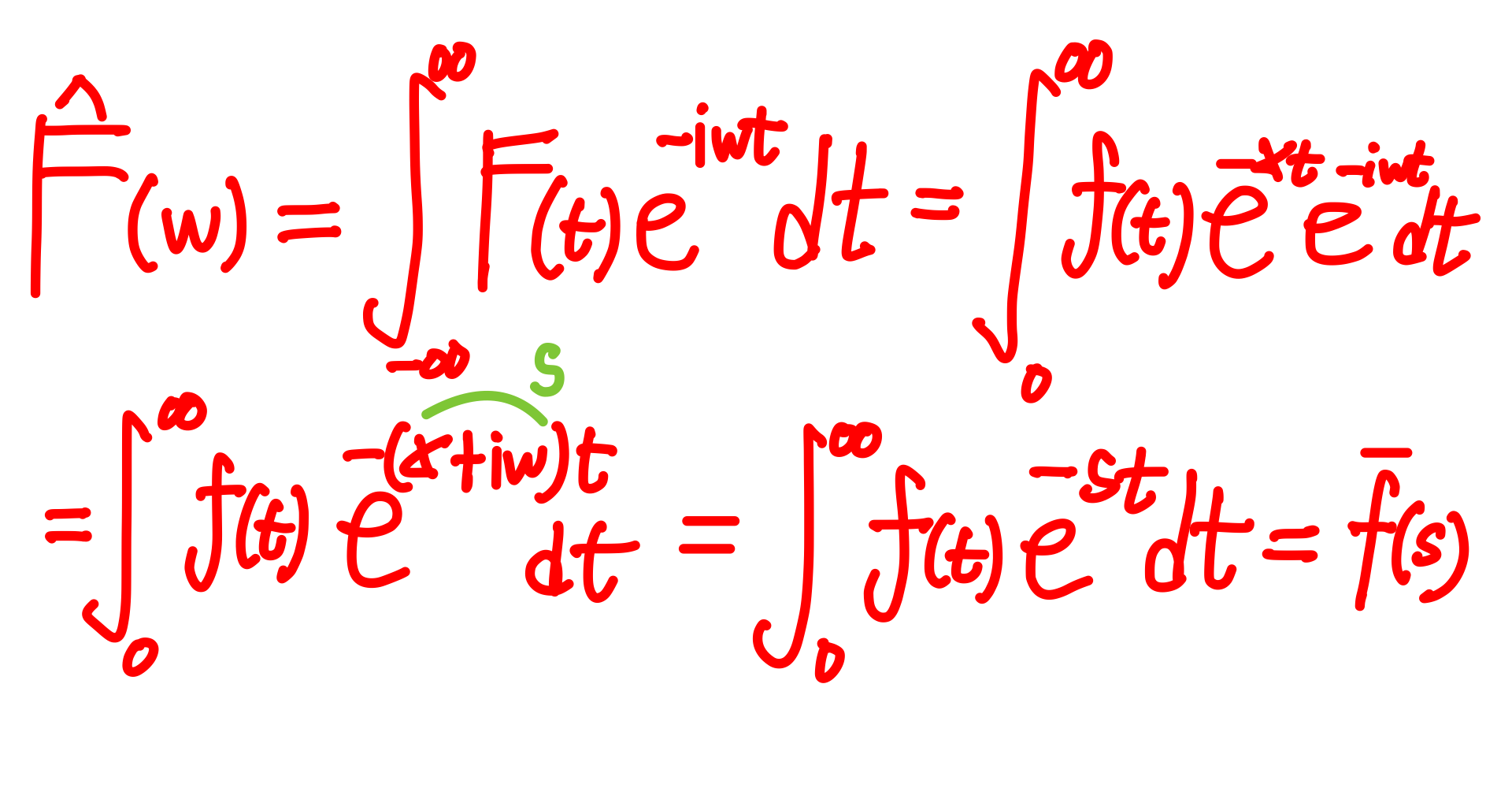
- 라플라스 역변환
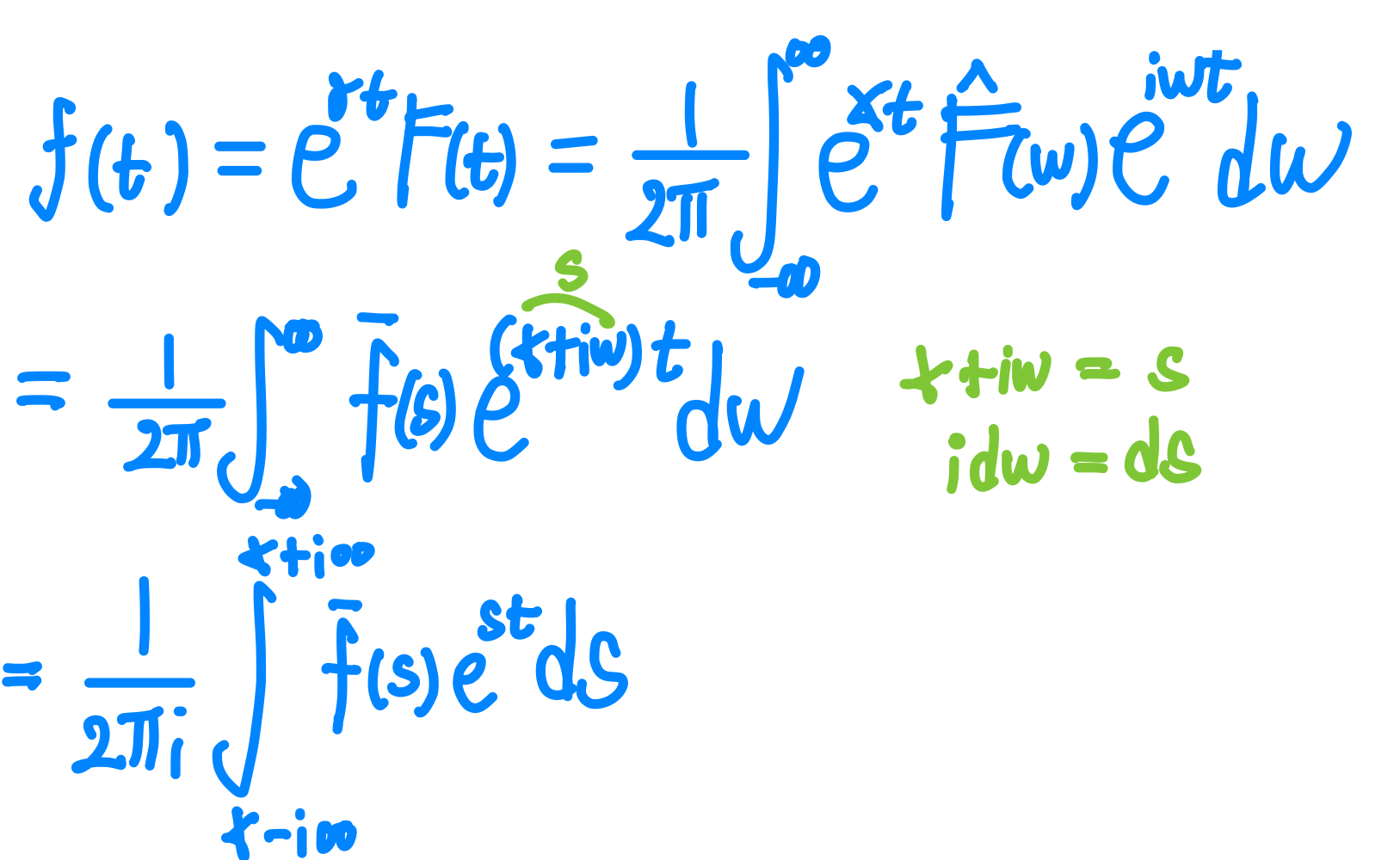
- 라플라스 pair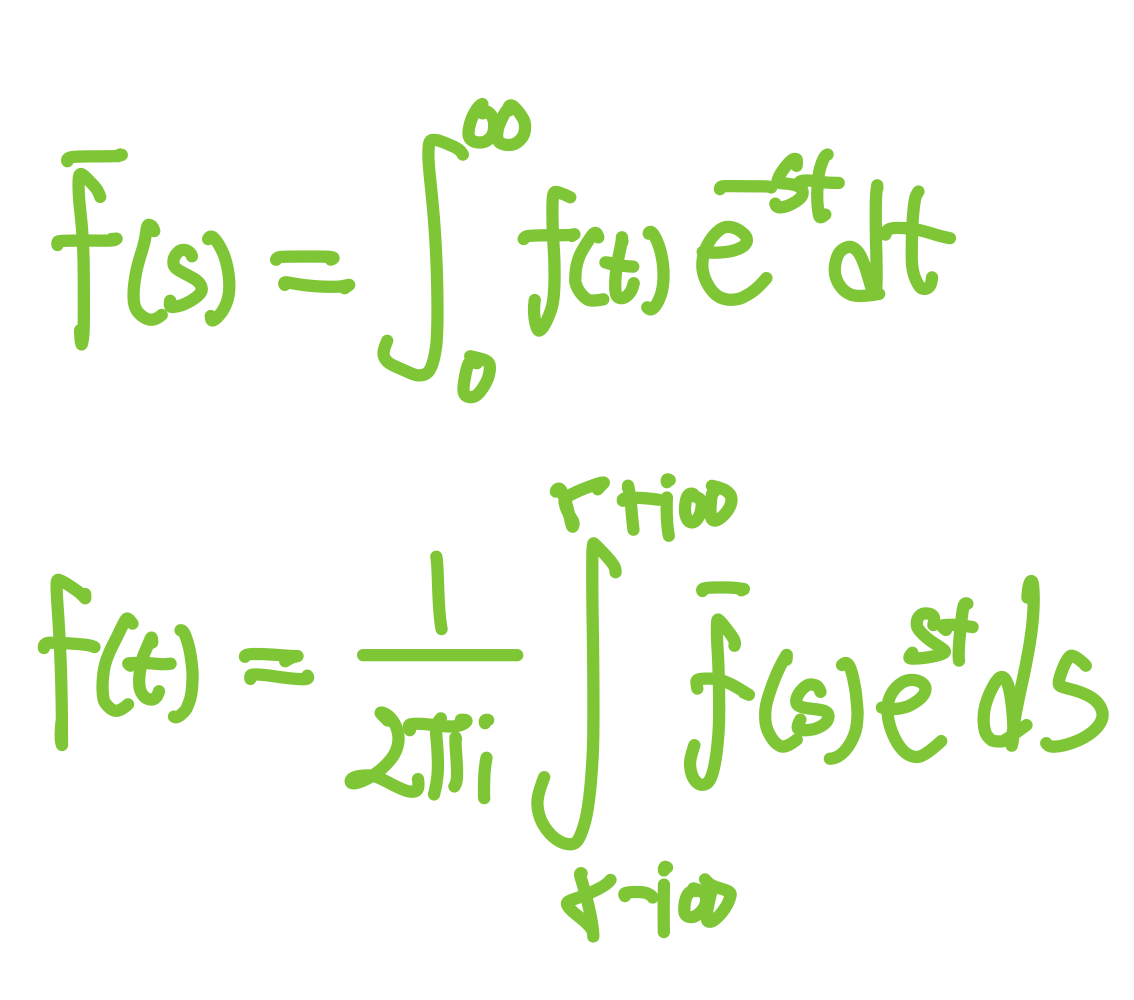
'Math♾️ > Fourier Analysis' 카테고리의 다른 글
컨볼루션(합성 곱) 에 대한 직관적 이해 (3) 2023.05.15 라플라스 변환 주요 사항 정리 (0) 2022.09.23 Wavelets and Multi resolution Analysis (0) 2022.09.22 불확정성의 원리 with Fourier Transform (0) 2022.09.21 The Spectrogram and the Gabor Transform (0) 2022.09.21