선형 시스템 파이썬으로 표현하기
아래와 같은 2차 선형시스템을 생각해 보자
$$A\vec{v} = \vec{b}$$
## numpy와 matplot library import (필요한 라이브러리 import)
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
## 그래프 polt시 사용할 색 지정
mpl.rcParams['axes.prop_cycle'] = mpl.cycler(color=["#377eb8","#ff7f00", "#4daf4a",
"#e41a1c", "#984ea3", "#a65628"])
$$\begin{pmatrix} 2&-1 \\ 1&1 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix} =
\begin{pmatrix}1 \\5\end{pmatrix}$$
$A$는 2X2 행렬이고, $\vec{v}$ 와 $\vec{b}$는 1X2 벡터이다.
행 관점에서 보기
위의 선형시스템을 행 관점에서 분석해보면 다음과 같이 해당 시스템은 두 선형 방정식으로 구성되어 있는 것을 알 수 있다. $$\begin{cases} 2x-y=1\\x+y=5\\ \end{cases}$$
각 선형 방정식은 좌표축상에서 표현하면 직선의 형태로 나타나며 두 직선의 교점(만나는 점)을 구하면 $(2,3)$ 이다.
## 행관점에서 보기
# 2x - y = 1
# x + y = 5
## 방정식 구성하기
x = np.array([-5, 5]) # x축 범위는 -5 부터 5까지이며
# 해당 범위에서 y1과 y2는 다음과 같이 나타낸다.
y1 = 2*x - 1
y2 = 5 - x
## 직선의 방정식 그리기
plt.figure(figsize=(4, 4), facecolor="w") # figure 크기와 색 설정
plt.plot(x, y1, x, y2) # figure상에 직선의 방정식 그리기
# 교점 나타내기
plt.plot(2, 3, "ro", mec="r")
plt.title("2d row picture") # 그래프 제목
## 좌표축 이름 붙이기
plt.xlabel("x")
plt.ylabel("y", rotation=0)
plt.xlim(x) # x축범위
plt.ylim(ymin=-10) # y축 범위
plt.grid(True) # 눈금 나타내기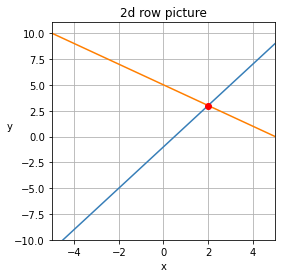
행 관점에서 해석하면 해당 시스템은 두개의 선형 방정식으로 구성되어 있으며
각 선형 방정식은 같은 input을 주었을 때 다른 기울기를 가지면서 output의 방향성(+,-)가 반대인 것을 알 수 있다.
그리고 교차점을 가지며 해석하는 시스템이 의미하는 바에 따라 해당 교점에 대한 다양한 해석이 가능하다.
열 관점에서 보기
열관점에서 위의 시스템을 보면 행렬 $A\vec{v}$는 두 열벡터의 선형결합으로 해석할 수 있다.
행관점에서는 두 선형방정식를 모두 만족 시키는 해가 교차점이며 그 값이 $(x,y)$ 이었다면
열관점에서는 행렬 $A$을 구성하는 두 열벡터 $\begin{pmatrix}2\\1\end{pmatrix} \begin{pmatrix}-1\\1\end{pmatrix}$가 선형 결합을 통하여 $\vec{b} = \begin{pmatrix}1\\5\end{pmatrix}$가 되기 위해서 필요한 스칼라배 값이 $x,y$가 되는 것이다.
$$x\begin{pmatrix}2\\1\end{pmatrix} + y\begin{pmatrix}-1\\1\end{pmatrix} = \begin{pmatrix}1\\5\end{pmatrix}$$
열 관점에서의 해석을 좀 더 이해하기 쉽게 그림으로 나타내면 다음과 같다.
## 열관점에서 보기
# 행렬 A를 두개의 열벡터의 묶음으로 보면
v1 = np.array([2, 1]) ## 첫번째 열벡터 (2,1)
v2 = np.array([-1, 1]) ## 두번째 열벡터 (-1,1)
lc = 2*v1 + 3*v2 ## 벡터 b -> 두 열벡터의 선형결합을 통해 벡터 b를 얻기 위해서 (x,y)는 (2,3)
# 각 열벡터와 열벡터의 선형 결합 결과 그리기
plt.clf()
# 시점(0,0),배열 첫번째 원소-(벡터의 x축 방향 값),배열 두번째 원소-(벡터의 y축 방향 값)
plt.arrow(0, 0, v1[0], v1[1], color="#377eb8")
plt.arrow(0, 0, v2[0], v2[1], color="#ff7f00")
plt.arrow(0, 0, lc[0], lc[1], color="#e41a1c")
# figure이름과 좌표축 이름 설정하기
plt.title("2d column picture")
plt.text(2.1, 1.1, r"$v_1$", color="#377eb8")
plt.text(-1.3, 1.1, r"$v_2$", color="#ff7f00")
plt.text(1.1, 5.1, r"$2 v_1 + 3 v_2$", color="#e41a1c")
plt.xlim((-3, 3))
plt.ylim((-0.5, 5.5))
plt.grid(True)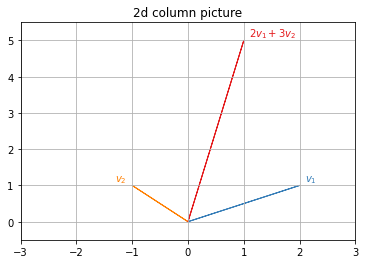
위의 그림으로 보면 열 관점의 해석이 무엇인지 알 수 있다.
시스템 $A$를 열벡터의 묶음으로 보고
각 열벡터의 선형 결합을 통하여 해당 시스템에서 나타날 수 있는 결과를 표현하는 것이다.
행 관점보다 열 관점으로 보았을 때 공간 상에서의 벡터들의 선형 결합으로서
선형 시스템에 대하여 좀 더 직관적으로 이해할 수 있으며
직관에 의한 확장적 사고를 가능하게 한다.
따라서 선형 시스템 해석시에는 열관점이 선호된다.
열 벡터 공간 시각화
열 벡터 관점에서 보았다시피 시스템을 열벡터의 묶음으로 보고
해당 시스템에서 나타날 수 있는 결과들을 열 벡터들의 선형 결합으로 나타낼 수 있다.
따라서 열 벡터 공간은 해당 시스템에서 나타날 수 있는 결과들의 집합이라 할 수 있다.
## 두 열벡터의 선형 결합으로 나타날 수 있는 열 공간 나타내기
v1 = np.array([2, 1]) # 시스템을 구성하는 열벡터 1
v2 = np.array([-1, 1]) # 시스템을 구성하는 열벡터 2
a = np.column_stack((v1, v2)) # 열벡터 1,2의 선형 결합으로 나타나는 열공간 a
## 열 공간 나타내는 범위 (min,max,num)
xvals = np.linspace(-3, 3, 31)
yvals = np.linspace(-3, 3, 31)
# 입력이될 grid 만들기
grid = np.column_stack([[x, y] for x in xvals for y in yvals])
# 열공간과 grid 선형변환
lc = np.dot(a, grid)
# 열 벡터 선형결합으로 열공간 나타내기
plt.clf()
plt.plot(lc[0], lc[1], ".", color="#4daf4a", ms=2)
plt.arrow(0, 0, v1[0], v1[1], color="#377eb8", lw=2)
plt.arrow(0, 0, v2[0], v2[1], color="#ff7f00", lw=2)
plt.title("Column space visualization")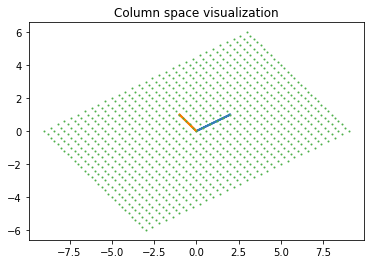
선형 시스템 해 구하기
파이썬을 이용해서 선형 시스템의 해를 다음과 같이 구할 수 있다.
a = np.array([[2, -1], [1, 1]]) # 시스템을 나타내는 행렬A
b = np.array([1, 5]) # 해당 시스템에서 얻고자 하는 결과
sol = np.linalg.solve(a, b) # 선형시스템 해 구하기
print(sol) # 값 출력
#결과 : [2. 3.]★ 출처
01. Linear systems in 2D
Develop geometrical intuition for a 2D linear system Av=b Av = b Av=b where A A A is a 2-by-2 matrix, and v v v and b b b are 2-by-1 column vectors Setup Start a python shell and import libraries: import numpy as np import matplotlib as mpl import matplotl
dododas.github.io